题目内容

若|z+i|+|z-i|=4，则复平面内与复数z对应的点的轨迹是（　　）
A、线段B、椭圆C、双曲线D、圆
考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：转化复数方程为复平面点的几何意义，然后判断轨迹即可．
解答： 解：|z+i|+|z-i|=4的几何意义是：复数z在复平面上对应点到（0，1）与（0，-1）的距离之和，而且距离之和大于两点的距离，所以z的轨迹满足椭圆的定义．
故选：B．
点评：本题考查轨迹方程的求法与轨迹的判断，椭圆的定义的应用，基本知识的考查．
练习册系列答案
相关题目
设函数f（x）的定义域、值域分别为A，B，且A∩B是单元集，下列命题：
①若A∩B={a}，则f（a）=a；
②若f（x）具有奇偶性，则f（x）可能为偶函数；
③若B不是单元集，则满足f[f（x）]=f（x）的x值可能不存在；
④若f（x）不是常数函数，则f（x）不可能为周期函数；其中，正确命题的序号为
 
．
为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老人，结果如下：
您是否需要志愿者男女
需要4030
不需要160270
（Ⅰ）估计该地区老年人中，需要志愿提供帮助的老年人的比例；
（Ⅱ）通过计算说明，你能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？
附：
P(K2≥k)
k
 
0.050
3.841
 
0.010
6.625
  
0.001
10.828
    K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
．
给出以下命题：
①i是虚数单位，复数
2i
1+i
的实部为1；
②命题p：“?x∈R+，sinx+
1
sinx
≥2”是真命题；
③已知线性回归方程为
?
y
=3+2x，当变量x增加2个单位，其预报值平均增加4个单位；
④把函数y=3sin（2x+
π
3
）的图象按向量
n
=（
π
3
，1）平移后得到y=1+3sin2x的图象；
⑤已知
2
2-4
+
6
6-4
=2，
5
5-4
+
3
3-4
=2，
7
7-4
+
1
1-4
=2，
10
10-4
+
-2
-2-4
=2，依照以上各式的规律，得到一般性的等式为
n
n-4
+
8-n
(8-n)-4
=2，（n≠4）．
则正确命题的序号为
 
（写出所有正确命题的序号）．
设α，β为两个不重合的平面，m，n是两条不重合的直线，给出下列四个命题：
①若m⊥n，m⊥α，则n∥α；
②若n?α，m?β，α与β相交且不垂直，则n与m不垂直；
③若α⊥β，α∩β=m，m⊥n，则n⊥β；
④若m∥n，n⊥α，α∥β，则m⊥β．
其中所有真命题的序号
 
．
将y=f′（x）sinx图象向左平移
π
4
个单位，得y=1-2sin2x图象，则f（x）=（　　）
A、2cosxB、2sinx
C、sinxD、cosx
函数f（x）的图象如图所示，下列数值排序正确的是（　　）
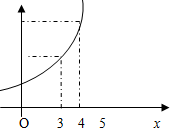
A、0＜f′（3）＜f′（4）＜f（4）-f（3）
B、0＜f′（3）＜f（4）-f（3）＜f′（4）
C、0＜f′（4）＜f′（3）＜f（4）-f（3）
D、0＜f（4）-f（3）＜f′（3）＜f′（4）
已知cosβ=-
1
3
，sin（α+β）=
7
9
，且α∈（0，
π
2
），β∈（
π
2
，π），求cosα的值．
有一段“三段论”推理：对于可导函数f（x），若f（x）在区间（a，b）上是增函数，则f′（x）＞0对x∈（a，b）恒成立，因为函数f（x）=x3在R上是增函数，所以f（x）=3x2＞0对x∈R恒成立．以上推理中（　　）
A、大前提错误
B、小前提错误
C、推理形式错误
D、推理正确

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网