Question

已知A（x₁，y₁），B（x₂，y₂）（x₁＞x₂）是函数f（x）=x³-|x|图象上的两个不同点，且在A，B两点处的切线互相平行，则

x2

x1

的取值范围为

 

．

Answer 1

考点：利用导数研究曲线上某点切线方程

专题：创新题型

分析：首先把含有绝对值的函数写成分段函数的形式，然后求导，通过在A，B两点处的切线互相平行，即在A，B两点处的导数值相等，分析出A点在y轴的右侧，B点在y轴的左侧．根据A，B两点处的导数相等，得到x₁与x₂的关系式，根据关系式得出它表示的曲线，然后利用式子的几何意义求解．

解答： 解：由题意，f（x）=x³-|x|=

x3-x， x≥0 x3+x， x＜0

，
   当x≥0时，f′（x）=3x²-1，
   当x＜0时，f′（x）=3x²+1，
  因为在A，B两点处的切线互相平行，且x₁＞x₂，
  所以x₁＞0，x₂＜0 （否则根据导数相等得出A、B两点重合），
  所以在点A（x₁，y₁）处切线的斜率为f′（x₁）=3x12-1，
  在点B（x₂，y₂）处切线的斜率为f′（x₂）=3x22+1
  所以3x12-1=3x22+1，
  即

x12

2 3

-

x22

2 3

=1，（x₁＞x₂，x₂＜0）
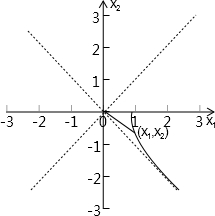
  表示的曲线为双曲线在第四象限的部分，如图：
 

x2

x1

表示这个曲线上的点与原点连线的斜率，
  由图可知

x2

x1

取值范围是（-1，0），故答案为：（-1，0）．

点评：本题考查了导数在研究切线方面的应用，同时考查了数形结合的思想，综合性较强，难度较大．本题的关键是把问题转化成图形的几何意义求解．