题目内容
P为曲线C1：
，（θ为参数）上一点，则它到直线C2：
（t为参数）距离的最小值为 ．
|
|
考点：参数方程化成普通方程
专题：坐标系和参数方程
分析：首先，将曲线C1和曲线C2化为普通方程，然后，求解最小值即可．
解答：
解：将曲线C1化成普通方程是（x-1）2+y2=1，
圆心是（1，0），
直线C2化成普通方程是y-2=0，
则圆心到直线的距离为2，
∴曲线C1上点到直线的距离为1，该点为（1，1），
故答案为：1．
圆心是（1，0），
直线C2化成普通方程是y-2=0，
则圆心到直线的距离为2，
∴曲线C1上点到直线的距离为1，该点为（1，1），
故答案为：1．
点评：本题重点考查了曲线的参数方程、曲线的普通方程及其互化等知识，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
正三棱锥的底面周长为6，侧面都是直角三角形，则此棱锥的体积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知某个几何体的三视图如图所示，根据图中标出的尺寸，可得这个几何体的体积是（ ）
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
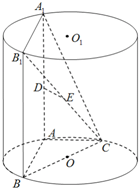如图，AA1、BB1为圆柱OO1的母线，BC是底面圆O的直径，D，E分别是AA1、CB1的中点，DE⊥面CBB1．
如图，已知直线l与半径为1的⊙D相切于点C，动点P到直线l的距离为d，若d=在30瓶饮料中，有3瓶已过了保质期．从这30瓶饮料中任取2瓶，则至少取到一瓶已过保质期饮料的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|