题目内容
已知ax2-b=0是关于x的一元二次方程,其中a、b∈{1,2,3,4},解集不同的一元二次方程的个数为 .
考点:排列、组合及简单计数问题
专题:排列组合
分析:先任意选两个,可以重复,共有16种,再排除相等的,问题得以解决
解答:
解:因为ax2-b=0,所以x2=
,
从{1,2,3,4},任意取两个,共有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共有4×4=16种,其中(1,1),(2,2),(3,3),(4,4)中
=1,(1,2),(2,4)中
=2,(2,1),(4,2)中
=
,
故
不同的个数为16-3-1-1=11
故解集不同的一元二次方程的个数为11个,
故答案为:11
| b |
| a |
从{1,2,3,4},任意取两个,共有(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)共有4×4=16种,其中(1,1),(2,2),(3,3),(4,4)中
| b |
| a |
| b |
| a |
| b |
| a |
| 1 |
| 2 |
故
| b |
| a |
故解集不同的一元二次方程的个数为11个,
故答案为:11
点评:本题考查了排列组合中的数字问题,关键是不要忘了需要排除
的值相等的情况,属于基础题
| b |
| a |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设四面体ABCD的六条棱的长分别为1,1,
,
,
和
,则其外接球的表面积为( )
| 2 |
| 2 |
| 2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
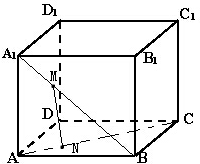 已知正方体ABCD-A1B1C1D1的棱长为a,M、N分别为A1B和AC上的点,A1M=AN=
已知正方体ABCD-A1B1C1D1的棱长为a,M、N分别为A1B和AC上的点,A1M=AN=