题目内容
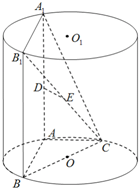 如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1、CB1的中点,DE⊥面CBB1.
如图,AA1、BB1为圆柱OO1的母线,BC是底面圆O的直径,D,E分别是AA1、CB1的中点,DE⊥面CBB1.(1)证明:DE∥面ABC;
(2)求四棱锥C-ABB1A1与圆柱OO1的体积比;
(3)若BB1=BC,求CA1与面BB1C所成角的正弦值.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积,直线与平面所成的角
专题:空间位置关系与距离
分析:(1)先证明四边形AOED是平行四边形,即可得到 DE∥OA,从而证得DE∥面ABC.
(2)由CA⊥AB,且AA1⊥CA,可得CA⊥面AA1B1B,即CA为四棱锥的高,设圆柱高为h,底半径为r,则V柱=πr2h,求出椎体的体积,即可得到四棱锥C-ABB1A1与圆柱OO1的体积比.
(3)先证 A1O1⊥面CBB1C1,则∠A1CO1为CA1与面BB1C所成的角,在Rt△A1O1C中,由sin∠A1CO1=
求得CA1与面BB1C所成角的正弦值.
(2)由CA⊥AB,且AA1⊥CA,可得CA⊥面AA1B1B,即CA为四棱锥的高,设圆柱高为h,底半径为r,则V柱=πr2h,求出椎体的体积,即可得到四棱锥C-ABB1A1与圆柱OO1的体积比.
(3)先证 A1O1⊥面CBB1C1,则∠A1CO1为CA1与面BB1C所成的角,在Rt△A1O1C中,由sin∠A1CO1=
| A1O1 |
| A1C |
解答:
解:(1)证明:连接EO,OA.∵E,O分别为B1C,BC的中点,∴EO∥BB1.
又DA∥BB1,且DA=EO=
BB1.∴四边形AOED是平行四边形,
即DE∥OA,DE?面ABC.∴DE∥面ABC.
(2)由题DE⊥面CBB1,且由(1)知DE∥OA.∴AO⊥面CBB1,∴AO⊥BC,
∴AC=AB.因BC是底面圆O的直径,得CA⊥AB,且AA1⊥CA,
∴CA⊥面AA1B1B,即CA为四棱锥的高.
设圆柱高为h,底半径为r,则V柱=πr2h,V锥=
h•(
r)•(
r)=
hr2,
∴V锥:V柱 =
.
(3)解:作过C的母线CC1,连接B1C1,则B1C1是上底面圆O1的直径,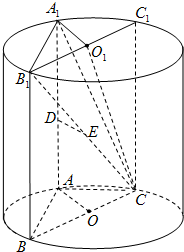
连接A1O1,得A1O1∥AO,又AO⊥面CBB1C1,
∴A1O1⊥面CBB1C1,连接CO1,
则∠A1CO1为CA1与面BB1C所成的角,
设BB1=BC=2,则A1C=
,
A1O1=1.(12分)
在Rt△A1O1C中,sin∠A1CO1=
=
.
又DA∥BB1,且DA=EO=
| 1 |
| 2 |
即DE∥OA,DE?面ABC.∴DE∥面ABC.
(2)由题DE⊥面CBB1,且由(1)知DE∥OA.∴AO⊥面CBB1,∴AO⊥BC,
∴AC=AB.因BC是底面圆O的直径,得CA⊥AB,且AA1⊥CA,
∴CA⊥面AA1B1B,即CA为四棱锥的高.
设圆柱高为h,底半径为r,则V柱=πr2h,V锥=
| 1 |
| 3 |
| 2 |
| 2 |
| 2 |
| 3 |
∴V锥:V柱 =
| 2 |
| 3π |
(3)解:作过C的母线CC1,连接B1C1,则B1C1是上底面圆O1的直径,

连接A1O1,得A1O1∥AO,又AO⊥面CBB1C1,
∴A1O1⊥面CBB1C1,连接CO1,
则∠A1CO1为CA1与面BB1C所成的角,
设BB1=BC=2,则A1C=
| 6 |
A1O1=1.(12分)
在Rt△A1O1C中,sin∠A1CO1=
| A1O1 |
| A1C |
| ||
| 6 |
点评:本题考查证明线面平行的方法,求棱锥的体积和直线与平面成的角,找出∠A1CO1为CA1与面BB1C所成的角,是解题的难点.

练习册系列答案
相关题目
如果
<θ<
,那么下列各式中正确的是( )
| π |
| 4 |
| π |
| 2 |
| A、cosθ<tanθ<sinθ |
| B、sinθ<cosθ<tanθ |
| C、tanθ<sinθ<cosθ |
| D、cosθ<sinθ<tanθ |
已知θ是三角形的一个内角,且sinθ+cosθ=
,则x2sinθ-y2cosθ=1表示( )
| 1 |
| 2 |
| A、焦点在x轴上的椭圆 |
| B、焦点在x轴上的双曲线 |
| C、焦点在y轴上的椭圆 |
| D、焦点在y轴上的双曲线 |
函数f(x)=sin(ωx+
)(ω>0)的最小正周期为π,则该函数图象( )
| π |
| 3 |
A、关于直线x=
| ||
B、关于直线x=
| ||
C、关于点(
| ||
D、关于点(
|
某外商计划在5个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有( )
| A、60种 | B、70种 |
| C、80种 | D、120种 |
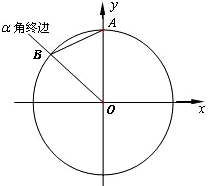 如图所示,单位圆(半径为1)的圆心O为坐标原点,它与y轴的正半轴交于点A,与钝角α的终边交于点B(xB,yB),设∠BAO=β,sin2β=
如图所示,单位圆(半径为1)的圆心O为坐标原点,它与y轴的正半轴交于点A,与钝角α的终边交于点B(xB,yB),设∠BAO=β,sin2β=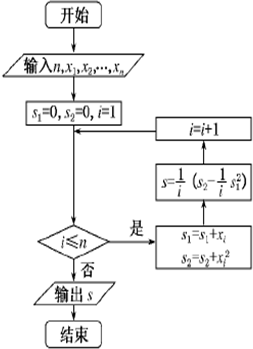 某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,…,xn(单位:吨).根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的结果s为
某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,…,xn(单位:吨).根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的结果s为