题目内容
已知某个几何体的三视图如图所示,根据图中标出的尺寸,可得这个几何体的体积是( )

A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知中的三视图可得该几何体是一个三棱柱,求出棱柱的底面面积和高,代入棱柱体积公式,可得答案.
解答:
解:由已知中的三视图可得该几何体是一个三棱柱,
其底面面积S=
×2×1=1,
高h=1,
故棱柱的体积V=Sh=1,
故选:B
其底面面积S=
| 1 |
| 2 |
高h=1,
故棱柱的体积V=Sh=1,
故选:B
点评:本题考查的知识点是由三视图求体积和表面积,根据已知中的三视图,判断出几何体的形状是解答的关键.

练习册系列答案
相关题目
已知等差数列{an}的前n项和为Sn,a1+a5=2,且a9=19,则S11=( )
| A、260 | B、220 |
| C、130 | D、110 |
如果
<θ<
,那么下列各式中正确的是( )
| π |
| 4 |
| π |
| 2 |
| A、cosθ<tanθ<sinθ |
| B、sinθ<cosθ<tanθ |
| C、tanθ<sinθ<cosθ |
| D、cosθ<sinθ<tanθ |
函数f(x)=sin(ωx+
)(ω>0)的最小正周期为π,则该函数图象( )
| π |
| 3 |
A、关于直线x=
| ||
B、关于直线x=
| ||
C、关于点(
| ||
D、关于点(
|
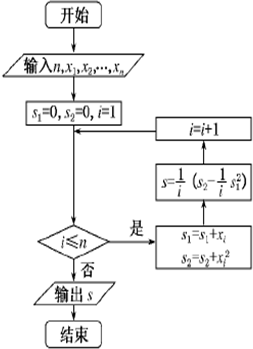 某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,…,xn(单位:吨).根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的结果s为
某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中n位居民的月均用水量分别为x1,…,xn(单位:吨).根据如图所示的程序框图,若n=2,且x1,x2分别为1,2,则输出的结果s为