Question

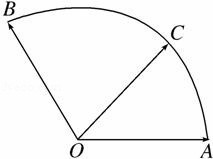给定两个平面向量

OA

和

OB

，它们的夹角为120°．点C在以O为圆心的圆弧AB上，且

OC

=x

OA

+y

OB

，其中x，y∈R，则满足x+y≥

2

的概率为

 

．

Answer 1

考点：几何概型

专题：概率与统计

分析：根据题意，建立坐标系，设出A，B点的坐标，并设∠AOC=α，则由

OC

=x

OA

+y

OB

得x，y的值，从而求得x+y，结合正弦函数的性质可求满足条件的角α的范围，利用几何概型的概率公式即可得到结论．

解答： 解：建立如图所示的坐标系，
则A（1，0），B（cos120°，sin120°），即B（-

1

2

，

3

2

），
设∠AOC=α，则

OC

=（cosα，sinα）
∵

OC

=x

OA

+y

OB

=（x，0）+（-

1

2

y，

3

2

y）=（cosα，sinα）．
∴

x- 1 2 y=cosα 3 y 2 =sinα

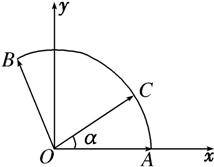
，即

x= sinα 3 +cosα y= 2sinα 3

，
∴x+y=

3

sinα+cosα=2sin（α+30°）．
∵0°≤α≤120°．
∴30°≤α+30°≤150°．
当x+y≥

2

时，sin（α+30°）≥

2

2

∴45°≤α+30°≤135°，
即15°≤α≤105°，
∴满足x+y≥

2

的概率P=

105°-15°

120°

=

3

4

，
故答案为：

3

4

点评：本题主要考查几何概型的计算，根据三角函数的对应转化为角度之间的关系是解决本题的关键，本题综合性较强，难度较大．