题目内容
设函数f(x)=alnx-bx2,其图象在点P(2,f(2))处切线的斜率为-3.
(1)求函数f(x)的单调区间(用只含有b的式子表示);
(2)当a=2时,令g(x)=f(x)-kx,设x1,x2(x1<x2)是函数g(x)=0的两个根,x0是x1,x2的等差中项,求证:g′(x0)<0(g′(x)为函数g(x)的导函数).
(1)求函数f(x)的单调区间(用只含有b的式子表示);
(2)当a=2时,令g(x)=f(x)-kx,设x1,x2(x1<x2)是函数g(x)=0的两个根,x0是x1,x2的等差中项,求证:g′(x0)<0(g′(x)为函数g(x)的导函数).
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)由函数图象在在点P(2,f(2))处切线的斜率为-3得到a与b的关系,用b表示a,代入导函数解析式,然后分b=0,b<0,b>0分类求解函数的单调区间;
(2)由a的值求解b的值,得到函数g(x)的解析式,把函数的两个零点代入函数所对应的方程,求解得到k的值,求出g′(x0),借助于等差中项的概念把x0用x1,x2表示,换元后进一步利用导数研究函数的单调性,由单调性说明g′(x0)<0成立.
(2)由a的值求解b的值,得到函数g(x)的解析式,把函数的两个零点代入函数所对应的方程,求解得到k的值,求出g′(x0),借助于等差中项的概念把x0用x1,x2表示,换元后进一步利用导数研究函数的单调性,由单调性说明g′(x0)<0成立.
解答:
(1)解:函数f(x)的定义域为(0,+∞).
f′(x)=
-2bx,则f′(2)=
-4b=-3,即a=8b-6.
于是f′(x)=
.
①当b=0时,f′(x)=
<0,f(x)在(0,+∞)上是单调减函数;
②当b<0时,令f'(x)=0,得x=
(负舍),
∴f(x)在(0 ,
)上是单调减函数,在(
, +∞)上是单调增函数;
③当b>0时,若0<b≤
,则f'(x)<0恒成立,f(x)在(0,+∞)上单调减函数;
若b>
,令f'(x)=0,得x=
(负舍),
∴f(x)在(0 ,
)上单调增函数,在(
, +∞)上单调减函数;
综上,若b<0,f(x)的单调减区间为(0 ,
),单调增区间为(
, +∞);
若0≤b≤
,f(x)的单调减区间为(0,+∞);
若b>
,f(x)的单调增区间为(0 ,
),单调减区间为(
, +∞).
(2)证明:∵a=2,a=8b-6,
∴b=1,即g(x)=2lnx-x2-kx.
∵g(x)的两零点为x1,x2,则
,
相减得:2(lnx1-lnx2)-(x12-x22)-k(x1-x2)=0,
∵x1≠x2,
∴k=
-(x1+x2),
于是g′(x0)=
-2x0-k=
-
=
[
-(lnx1-lnx2)]=
[
-ln
].
令t=
,t∈(0, 1),φ(t)=
-lnt=2-
-lnt,
则φ′(t)=
-
=
<0,则φ(t)在(0,1)上单调递减,
则φ(t)>φ(1)=0,
又
<0,则g'(x0)<0.命题得证.
f′(x)=
| a |
| x |
| a |
| 2 |
于是f′(x)=
| -2bx2+(8b-6) |
| x |
①当b=0时,f′(x)=
| -6 |
| x |
②当b<0时,令f'(x)=0,得x=
|
∴f(x)在(0 ,
|
|
③当b>0时,若0<b≤
| 3 |
| 4 |
若b>
| 3 |
| 4 |
|
∴f(x)在(0 ,
|
|
综上,若b<0,f(x)的单调减区间为(0 ,
|
|
若0≤b≤
| 3 |
| 4 |
若b>
| 3 |
| 4 |
|
|
(2)证明:∵a=2,a=8b-6,
∴b=1,即g(x)=2lnx-x2-kx.
∵g(x)的两零点为x1,x2,则
|
相减得:2(lnx1-lnx2)-(x12-x22)-k(x1-x2)=0,
∵x1≠x2,
∴k=
| 2(lnx1-lnx2) |
| x1-x2 |
于是g′(x0)=
| 2 |
| x0 |
| 4 |
| x1+x2 |
| 2(lnx1-lnx2) |
| x1-x2 |
=
| 2 |
| x1-x2 |
| 2(x1-x2) |
| x1+x2 |
| 2 |
| x1-x2 |
2(
| ||
|
| x1 |
| x2 |
令t=
| x1 |
| x2 |
| 2(t-1) |
| t+1 |
| 4 |
| t+1 |
则φ′(t)=
| 4 |
| (t+1)2 |
| 1 |
| t |
| -(t-1)2 |
| t(t+1)2 |
则φ(t)>φ(1)=0,
又
| 2 |
| x1-x2 |
点评:本题考查利用导数研究曲线上某点处的切线方程,考查了利用导数研究函数的单调性,考查了数学转化思想方法,训练了换元法,是难度较大的题目.

练习册系列答案
相关题目
已知函数f(x)是定义在R上的偶函数,它在[0,+∞)上是减函数.则下列各式一定成立的是( )
| A、f(0)<f(6) |
| B、f(-3)>f(2) |
| C、f(-1)>f(3) |
| D、f(-2)<f(-3) |
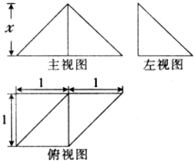 如图所示是一个几何体的三视图,若该几何体的体积为
如图所示是一个几何体的三视图,若该几何体的体积为| 1 |
| 2 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
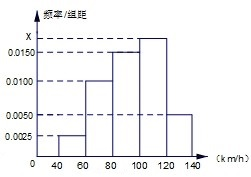 根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h~120km/h,则该时段内过往的这100辆机动车中属非正常行驶的有
根据某固定测速点测得的某时段内过往的100辆机动车的行驶速度(单位:km/h)绘制的频率分布直方图如图所示.该路段限速标志牌提示机动车辆正常行驶速度为60km/h~120km/h,则该时段内过往的这100辆机动车中属非正常行驶的有