题目内容
定义在R上的函数f（x），在[2，+∞）单调递增，对任意实数x恒有f（2+x）=f（2-x）成立，若f（x）＜f（x+2），则x的取值范围是 ．
考点：抽象函数及其应用,函数单调性的性质
专题：函数的性质及应用
分析：依题意知，函数y=f（x）关于直线x=2对称，通过对x范围的讨论分析，结合函数的单调性质即可求得x的取值范围．
解答：
解：∵f（2+x）=f（2-x），
∴函数y=f（x）关于直线x=2对称，
又f（x）在[2，+∞）单调递增，
∴f（x）在（-∞，2]上单调递减，
∴当x≥2时，f（x）＜f（x+2）恒成立；
当x+2≤2，即x≤0时，总有f（x）≥f（x+2），故f（x）＜f（x+2）恒不成立；
当0＜x＜2时，要使f（x）＜f（x+2）恒成立，必须点M（x+2，f（x+2））到直线x=2的距离大于点N（x，f（x））到直线x=2的距离，即（x+2）-2＞2-x，
解得：1＜x＜2；
综上所述，x的取值范围是：（1，+∞）．
故答案为：（1，+∞）．
∴函数y=f（x）关于直线x=2对称，
又f（x）在[2，+∞）单调递增，
∴f（x）在（-∞，2]上单调递减，
∴当x≥2时，f（x）＜f（x+2）恒成立；
当x+2≤2，即x≤0时，总有f（x）≥f（x+2），故f（x）＜f（x+2）恒不成立；
当0＜x＜2时，要使f（x）＜f（x+2）恒成立，必须点M（x+2，f（x+2））到直线x=2的距离大于点N（x，f（x））到直线x=2的距离，即（x+2）-2＞2-x，
解得：1＜x＜2；
综上所述，x的取值范围是：（1，+∞）．
故答案为：（1，+∞）．
点评：本题考查函数的对称性与单调性，考查分类讨论思想与等价转化思想的综合应用，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
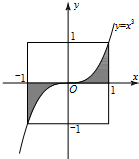如图，设D是图中边长为2的正方形区域，E是函数y=x3的图象与x轴及x=±1围成的阴影区域．向D中随机投一点，则该点落入E中的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|