题目内容
10.对函数f(x)=$\frac{cosx+m}{cosx+2}$,若?a,b,c∈R,f(a),f(b),f(c)都为某个三角形的三边长,则实数m的取值范围是( )| A. | ($\frac{5}{4}$,6) | B. | ($\frac{5}{3}$,6) | C. | ($\frac{7}{5}$,5) | D. | ($\frac{5}{4}$,5) |
分析 当m=2时,f(a)=f(b)=f(c)=1,是等边三角形的三边长;当m>2时,只要2(1+$\frac{m-2}{3}$)>m-1即可,当m<2时,只要1+$\frac{m-2}{3}$<2(m-1)即可,由此能求出结果,综合可得结论.
解答 解:函数f(x)=$\frac{cosx+m}{cosx+2}$,若?a,b,c∈R,f(a),f(b),f(c)都为某个三角形的三边长,
当m=2时,f(x)=$\frac{cosx+m}{cosx+2}$=1,
此时f(a)=f(b)=f(c)=1,是等边三角形的三边长,成立.
当m>2时,f(x)∈[1+$\frac{m-2}{3}$,m-1],
只要2(1+$\frac{m-2}{3}$)>m-1即可,解得2<m<5.
当m<2时,f(x)∈[m-1,1+$\frac{m-2}{3}$],
只要1+$\frac{m-2}{3}$<2(m-1)即可,解得$\frac{7}{5}$<m<2,
综上,实数m的取值范围($\frac{7}{5}$,5),
故选:C.
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意分类讨论思想的合理运用,属于中档题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
20.已知函数$f(x)=sinωx+\sqrt{3}cosωx$ (ω>0)的图象与直线y=-2的两个相邻公共点之间的距离等于π,则f(x)的单调递减区间是( )
| A. | $[kπ+\frac{π}{6},kπ+\frac{7π}{6}]k∈{Z}$ | B. | $[kπ+\frac{π}{12},kπ+\frac{7π}{12}]k∈{Z}$ | ||
| C. | $[kπ+\frac{π}{12},kπ+\frac{7π}{6}]k∈{Z}$ | D. | $[kπ-\frac{π}{12},kπ+\frac{7π}{12}]k∈{Z}$ |
1.已知A(1,3),B(4,-1),则与向量$\overrightarrow{AB}$共线的单位向量为( )
| A. | $({\frac{4}{5},\frac{3}{5}})$或$({-\frac{4}{5},\frac{3}{5}})$ | B. | $({\frac{3}{5},-\frac{4}{5}})$或$({-\frac{3}{5},\frac{4}{5}})$ | C. | $({-\frac{4}{5},-\frac{3}{5}})$或$({\frac{4}{5},\frac{3}{5}})$ | D. | $({-\frac{3}{5},-\frac{4}{5}})$或$({\frac{3}{5},\frac{4}{5}})$ |
18.已知空间四边形ABCD,链接AC,BD,则$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CD}$为( )
| A. | $\overrightarrow{AD}$ | B. | $\overrightarrow{BD}$ | C. | $\overrightarrow{AC}$ | D. | $\overrightarrow{0}$ |
2.已知数列{an}满足an=$\frac{1}{2}$an+1,若a3+a4=2,则a4+a5=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 4 | D. | 8 |
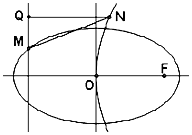 椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上有一点M(-4,$\frac{9}{5}$)在抛物线y2=2px(p>0)的准线l上,抛物线的焦点也是椭圆焦点.
椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上有一点M(-4,$\frac{9}{5}$)在抛物线y2=2px(p>0)的准线l上,抛物线的焦点也是椭圆焦点.