题目内容
19.已知数列{an}满足a1=1,且nan+1-(n+1)an=2n2+2n.(1)求a2,a3;
(2)证明数列{$\frac{{a}_{n}}{n}$}是等差数列,并求{an}的通项公式.
分析 (1)利用递推关系分别取n=1,2即可得出.
(2)由nan+1-(n+1)an=2n2+2n,看到$\frac{{a}_{n+1}}{n+1}$-$\frac{{a}_{n}}{n}$=2,即可证明.
解答 (1))解:由数列{an}满足a1=1,且nan+1-(n+1)an=2n2+2n.
∴a2-2×1=4,解得a2=6.
2a3-3×6=2×22+2×2,解得a3=15.
(2)证明:∵nan+1-(n+1)an=2n2+2n.
∴$\frac{{a}_{n+1}}{n+1}$-$\frac{{a}_{n}}{n}$=2,
∴数列{$\frac{{a}_{n}}{n}$}是等差数列,首项为1,公差为2.
∴$\frac{{a}_{n}}{n}$=1+2(n-1)=2n-1,
解得an=2n2-n.
点评 本题考查了等差数列的通项公式与求和公式、数列递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.对函数f(x)=$\frac{cosx+m}{cosx+2}$,若?a,b,c∈R,f(a),f(b),f(c)都为某个三角形的三边长,则实数m的取值范围是( )
| A. | ($\frac{5}{4}$,6) | B. | ($\frac{5}{3}$,6) | C. | ($\frac{7}{5}$,5) | D. | ($\frac{5}{4}$,5) |
7.已知函数f(x)=$\left\{\begin{array}{l}{2-|x|,x≤2}\\{(x-2)^{2},x>2}\end{array}\right.$函数g(x)=f(2-x)-$\frac{1}{4}$b,其中b∈R,若函数y=f(x)+g(x)恰有4个零点,则b的取值范围是( )
| A. | (7,8) | B. | (8,+∞) | C. | (-7,0) | D. | (-∞,8) |
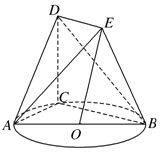 如图,点C是以AB为直径的圆上一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE=1,BC=2,AC=CD=3
如图,点C是以AB为直径的圆上一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE=1,BC=2,AC=CD=3