题目内容
18.已知空间四边形ABCD,链接AC,BD,则$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CD}$为( )| A. | $\overrightarrow{AD}$ | B. | $\overrightarrow{BD}$ | C. | $\overrightarrow{AC}$ | D. | $\overrightarrow{0}$ |
分析 根据向量的加减的几何意义即可求出.
解答 解:$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CD}$=$\overrightarrow{AC}$+$\overrightarrow{CD}$=$\overrightarrow{AD}$,
故选:A.
点评 本题考查向量的加法运算,以及向量加法的三角形法则和平行四边形法则,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.若sin(π-α)=-$\frac{{\sqrt{3}}}{3}$,且α∈(π,$\frac{3π}{2}$),则sin($\frac{π}{2}$+α)=( )
| A. | -$\frac{\sqrt{6}}{3}$ | B. | -$\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{6}}{6}$ | D. | $\frac{\sqrt{6}}{3}$ |
6.一个扇形OAB的面积为1平方厘米,它的周长为4厘米,则它的中心角是( )
| A. | 2弧度 | B. | 3弧度 | C. | 4弧度 | D. | 5弧度 |
13.已知函数f(x)=$\sqrt{2}$sinωx-$\sqrt{2}$cosωx(ω<0),若y=f(x+$\frac{π}{4}$)的图象与y=f(x-$\frac{π}{4}$)的图象重合,记ω的最大值为ω0,函数g(x)=cos(ω0x-$\frac{π}{3}$)的单调递增区间为( )
| A. | [-$\frac{1}{3}$π+$\frac{kπ}{2}$,-$\frac{π}{12}$+$\frac{kπ}{2}$](k∈Z) | B. | [-$\frac{π}{12}$+$\frac{kπ}{2}$,$\frac{π}{6}$+$\frac{kπ}{2}$](k∈Z) | ||
| C. | [-$\frac{1}{3}$π+2kπ,-$\frac{π}{12}$+2kπ](k∈Z) | D. | [-$\frac{π}{12}$+2kπ,-$\frac{π}{6}$+2kπ](k∈Z) |
3.在△ABC中,D为三角形所在平面内的一点,且$\overrightarrow{AD}$=$\frac{1}{3}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AC}$;则$\frac{{S}_{△BCD}}{{S}_{△ACD}}$=( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
10.对函数f(x)=$\frac{cosx+m}{cosx+2}$,若?a,b,c∈R,f(a),f(b),f(c)都为某个三角形的三边长,则实数m的取值范围是( )
| A. | ($\frac{5}{4}$,6) | B. | ($\frac{5}{3}$,6) | C. | ($\frac{7}{5}$,5) | D. | ($\frac{5}{4}$,5) |
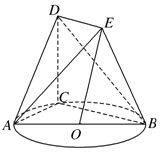 如图,点C是以AB为直径的圆上一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE=1,BC=2,AC=CD=3
如图,点C是以AB为直径的圆上一点,直角梯形BCDE所在平面与圆O所在平面垂直,且DE∥BC,DC⊥BC,DE=1,BC=2,AC=CD=3