Question

20．椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上有一点M（-4，$\frac{9}{5}$）在抛物线y²=2px（p＞0）的准线l上，抛物线的焦点也是椭圆焦点．
（1）求椭圆方程；
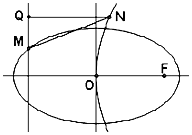
（2）若点N在抛物线上，过N作准线l的垂线，垂足为Q，求|MN|+|NQ|的最小值．

Answer 1

分析 （1）由题意求得c=4，得到p=8，再由点M（-4，$\frac{9}{5}$）在椭圆上，结合隐含条件求得a，b的值，则椭圆方程可求；
（2）由题意画出图形，由抛物线定义把|MN|+|NQ|的最小值转化为|MF|求解，由两点的距离公式，即可得到所求最小值．

解答 解：（1）∵椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1上的M（-4，$\frac{9}{5}$）
在抛物线y²=2px（p＞0）的准线l：x=-$\frac{p}{2}$上，
抛物线的焦点也是椭圆焦点．
∴c=4，p=8…①
∵M（-4，$\frac{9}{5}$）在椭圆上，
∴$\frac{16}{{a}^{2}}$+$\frac{81}{25{b}^{2}}$=1…②
又∵a²=b²+c²…③
∴由①②③解得：a=5，b=3，
∴椭圆为$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1；
（2）由p=8得抛物线为y²=16x．
设抛物线的焦点为F（4，0），由抛物线的定义得|NQ|=|NF|，
∴|MN|+|NQ|=|MN|+|NF|≥|MF|=$\sqrt{（-4-4）^{2}+（\frac{9}{5}-0）^{2}}$=$\frac{41}{5}$，即为所求的最小值．

点评 本题考查椭圆与抛物线的简单性质，考查了数学转化思想方法，运用三点共线取得最小值是解题的关键，考查运算能力，是中档题．