题目内容
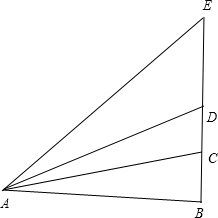
 如图,一小山峰BC的高为30cm,山顶上有建筑物CD的高为20cm,建筑物上竖一高为40m铁架DE,问在底面上距离B多远的地方,能找到这样一点A,使得∠BAC=∠DAE?
如图,一小山峰BC的高为30cm,山顶上有建筑物CD的高为20cm,建筑物上竖一高为40m铁架DE,问在底面上距离B多远的地方,能找到这样一点A,使得∠BAC=∠DAE?考点:解三角形的实际应用
专题:解三角形
分析:解:设距离Bxcm的地方,能找到这样一点A,使得∠BAC=∠DAE,则cos∠BAC=
,AD=
,AE=
,由余弦定理能求出在底面上距离B30
cm的地方,能找到这样一点A,使得∠BAC=∠DAE.
| x | ||
|
| x2+502 |
| x2+902 |
| 15 |
解答:
解:设距离Bxcm的地方,能找到这样一点A,使得∠BAC=∠DAE,
则cos∠BAC=
,AD=
,AE=
,
由余弦定理得cos∠EAO=
=
,
∴
=
,
整理,得x2(x2+2500)(x2+8100)=(x2+4500)2(x2+900),
解得x2=13500,或x2=-
(舍),
∴x=30
(cm).
∴在底面上距离B30
cm的地方,能找到这样一点A,
使得∠BAC=∠DAE.
则cos∠BAC=
| x | ||
|
| x2+502 |
| x2+902 |

由余弦定理得cos∠EAO=
| x2+2500+x2+8100-1600 | ||||
2
|
=
| 2x2+9000 | ||||
2
|
∴
| x | ||
|
| x2+4500 | ||||
|
整理,得x2(x2+2500)(x2+8100)=(x2+4500)2(x2+900),
解得x2=13500,或x2=-
| 13500 |
| 7 |
∴x=30
| 15 |
∴在底面上距离B30
| 15 |
使得∠BAC=∠DAE.
点评:本题考查三角形的边长的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.

练习册系列答案
相关题目
在(1+x)6(1+y)4的展开式中,记xmyn项的系数为f(m,n),则f(2,1)+f(1,2)=( )
| A、45 | B、60 | C、96 | D、108 |