题目内容
已知
是以点A(3,-1)为起点,且与向量
=(-3,4)平行的单位向量,则向量
的终点坐标是 .
| a |
| b |
| a |
考点:平面向量的坐标运算
专题:平面向量及应用
分析:首先,设向量
的终点坐标B(m,n),则
=(m-3,n+1),然后,根据共线和单位向量,建立等式,求解即可.
| a |
| a |
解答:
解:设向量
的终点坐标B(m,n),则
=(m-3,n+1),
∵
∥
,
∴(m-3)×4-(-3)(n+1)=0,①
∵
=1,②
联立①②,得
或
,
∴B(
,-
)或(
,-
).
故答案为:(
,-
)或(
,-
).
| a |
| a |
∵
| a |
| b |
∴(m-3)×4-(-3)(n+1)=0,①
∵
| (m-3)2+(n+1)2 |
联立①②,得
|
|
∴B(
| 12 |
| 5 |
| 1 |
| 5 |
| 18 |
| 5 |
| 9 |
| 5 |
故答案为:(
| 12 |
| 5 |
| 1 |
| 5 |
| 18 |
| 5 |
| 9 |
| 5 |
点评:本题重点考查了向量共线、向量的坐标表示、单位向量的概念等知识,考查了运算求解能力,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
各项都是正数的等比数列{an}的公比q≠1,且a2,
a3,a1成等差数列,则
的值为( )
| 1 |
| 2 |
| a3+a4+a5 |
| a4+a5+a6 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
某公司招收男职员x名,女职员y名,须满足约束条件
则10x+10y的最大值是( )
|
| A、80 | B、85 | C、90 | D、100 |
已知p:任意x∈R,不等式x2-mx+
>0恒成立;q:椭圆
+
=1的焦点在x轴上.
(1)若“p且q”为真命题,求实数m的取值范围;
(2)若“p或q”为真命题,求实数m的取值范围.
| 3 |
| 2 |
| x2 |
| m-1 |
| y2 |
| 3-m |
(1)若“p且q”为真命题,求实数m的取值范围;
(2)若“p或q”为真命题,求实数m的取值范围.
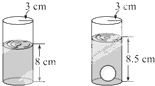 一个圆柱形的玻璃瓶的内半径为3cm,瓶里所装的水深为8cm,将一个钢球完全浸入水中,瓶中水的高度上升到8.5cm,则钢球的半径为( )
一个圆柱形的玻璃瓶的内半径为3cm,瓶里所装的水深为8cm,将一个钢球完全浸入水中,瓶中水的高度上升到8.5cm,则钢球的半径为( )| A、1 cm |
| B、1.2 cm |
| C、1.5 cm |
| D、2 cm |
 如图,一小山峰BC的高为30cm,山顶上有建筑物CD的高为20cm,建筑物上竖一高为40m铁架DE,问在底面上距离B多远的地方,能找到这样一点A,使得∠BAC=∠DAE?
如图,一小山峰BC的高为30cm,山顶上有建筑物CD的高为20cm,建筑物上竖一高为40m铁架DE,问在底面上距离B多远的地方,能找到这样一点A,使得∠BAC=∠DAE?