题目内容
已知函数f(x)=
,其中a,b∈R,e为自然对数的底数.
(1)当a=b=-3,求函数f(x)的单调递增区间;
(2)当x≤6时,若函数h(x)=f(x)-e-x(x3+b-1)存在两个相距大于2的极值点,求实数a的取值范围;
(3)若函数g(x)与函数f(x)的图象关于y轴对称,且函数g(x)在(-6,m),(2,n)上单调递减,在(m,2),(n,+∞)单调递增,试证明:f(n-m)<
.
|
(1)当a=b=-3,求函数f(x)的单调递增区间;
(2)当x≤6时,若函数h(x)=f(x)-e-x(x3+b-1)存在两个相距大于2的极值点,求实数a的取值范围;
(3)若函数g(x)与函数f(x)的图象关于y轴对称,且函数g(x)在(-6,m),(2,n)上单调递减,在(m,2),(n,+∞)单调递增,试证明:f(n-m)<
5
| ||
| 36 |
考点:利用导数研究函数的单调性,导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(1)当a=b=-3时,先求出f(x),然后对函数进行求导,结合导数即可判断函数的单调性;
(2)先求出当x<6时h(x)的解析式,求出h′(x),由h′(x)=0有两个相距大于2的根,列出所满足的不等式组,求出a的取值范围;
(3)写出g(x)的表达式,则x=2,x=n,x=m分别是g′(x)=0的三个根,得出m,n,a的关系,从而证明不等式成立.
(2)先求出当x<6时h(x)的解析式,求出h′(x),由h′(x)=0有两个相距大于2的根,列出所满足的不等式组,求出a的取值范围;
(3)写出g(x)的表达式,则x=2,x=n,x=m分别是g′(x)=0的三个根,得出m,n,a的关系,从而证明不等式成立.
解答:
(1)解:当x>6时,f(x)=
,则f′(x)=
<0,即f(x)在(6,+∞)单调递减;
当x≤6时,由已知,有f(x)=(x3+3x2-3x-3)e-x,f'(x)=-x(x-3)(x+3)e-x,知f(x)在(-∞,-3),(0,3)上单调递增,在(-3,0),(3,6)上单调递减.
综上,f(x)的单调递增区间为(-∞,-3)和(0,3).
(2)解:当x≤6时,h(x)=e-x(3x2+ax+1),h'(x)=e-x[-3x2-(a-6)x+a-1],
令φ(x)=3x2+(a-6)x+1-a,设其零点分别为x1,x2.
由
解得-
≤a<-2
或a>2
.
(3)证明:g(x)=
当x≥-6时,g'(x)=ex[-x3+(6-a)x+(b-a)],由g'(2)=0,得b=3a-4,
从而g'(x)=-ex[x3+(a-6)x+(4-2a)],因为g'(m)=g'(n)=0,
所以x3+(a-6)x+(4-2a)=(x-2)(x-m)(x-n),将右边展开,与左边比较系数得m+n=-2,mn=a-2,因为n>2,所以m<-4,n-m>6,又f(x)在[6,+∞)单调递减,则f(n-m)<f(6)=
,因为ln6<2,所以6ln6<12,(6ln6)2<144<150=(5
)2,即有6ln6<5
,
<
,从而f(n-m)<
.
| lnx |
| x |
| 1-lnx |
| x2 |
当x≤6时,由已知,有f(x)=(x3+3x2-3x-3)e-x,f'(x)=-x(x-3)(x+3)e-x,知f(x)在(-∞,-3),(0,3)上单调递增,在(-3,0),(3,6)上单调递减.
综上,f(x)的单调递增区间为(-∞,-3)和(0,3).
(2)解:当x≤6时,h(x)=e-x(3x2+ax+1),h'(x)=e-x[-3x2-(a-6)x+a-1],
令φ(x)=3x2+(a-6)x+1-a,设其零点分别为x1,x2.
由
|
| 73 |
| 5 |
| 3 |
| 3 |
(3)证明:g(x)=
|
当x≥-6时,g'(x)=ex[-x3+(6-a)x+(b-a)],由g'(2)=0,得b=3a-4,
从而g'(x)=-ex[x3+(a-6)x+(4-2a)],因为g'(m)=g'(n)=0,
所以x3+(a-6)x+(4-2a)=(x-2)(x-m)(x-n),将右边展开,与左边比较系数得m+n=-2,mn=a-2,因为n>2,所以m<-4,n-m>6,又f(x)在[6,+∞)单调递减,则f(n-m)<f(6)=
| ln6 |
| 6 |
| 6 |
| 6 |
| ln6 |
| 6 |
5
| ||
| 36 |
5
| ||
| 36 |
点评:本题考查利用导数求函数的单调区间,由零点求参数的取值范围,利用单调性证明不等式成立,试题有一定的难度.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
为了得到函数f(x)=cos(2x+
)的图象,只要把函数g(x)=
f′(x)的图象( )
| π |
| 4 |
| 1 |
| 2 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
设a>0,则
=( )
a•
|
A、
| |||
B、
| |||
C、
| |||
D、a
|
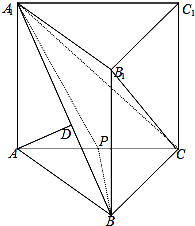 如图,直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.P为AC的中点.
如图,直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直线A1B上.P为AC的中点. 如图,在长方体ABCD-A′B′C′D′中,M、N分别为DD′,AD的中点,则图中阴影部分在平面ADD′A′上的射影为( )
如图,在长方体ABCD-A′B′C′D′中,M、N分别为DD′,AD的中点,则图中阴影部分在平面ADD′A′上的射影为( )


