题目内容
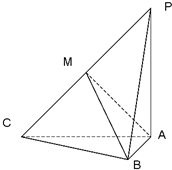 如图,三棱锥P-ABC中,
如图,三棱锥P-ABC中,| PA |
| AB |
| PA |
| AC |
| AB |
| AC |
| PA |
| AC |
| AB |
(I)求证:PC⊥平面MAB;
(Ⅱ)求二面角C-PB-A的余弦值.
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知得PA⊥AB,PA⊥AC,AB⊥AC,从而PA⊥AB,AB⊥PC,进而AM⊥PC,由此能证明PC⊥平面MAB.
(Ⅱ)以A为原点,AC为x轴,AB为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出二面角C-PB-A的余弦值.
(Ⅱ)以A为原点,AC为x轴,AB为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出二面角C-PB-A的余弦值.
解答:
(Ⅰ)证明:∵三棱锥P-ABC中,
•
=
•
=
•
=0,
2=
2=4
2,
∴PA⊥AB,PA⊥AC,AB⊥AC,PA=AC=2AB,
∴PA⊥平面ABC,∴PA⊥AB,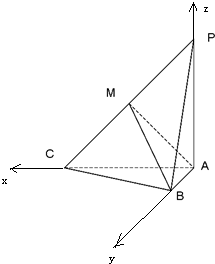
∴AB⊥平面PAC,∴AB⊥PC,
∵M为棱PC的中点,∴AM⊥PC,
又AM∩AB=A,∴PC⊥平面MAB.
(Ⅱ)解:以A为原点,AC为x轴,AB为y轴,AP为z轴,
建立空间直角坐标系,
设PA=AC=2AB=2,则C(2,0,0),P(0,0,2),
B(0,1,0),A(0,0,0),
=(2,0,-2),
=(0,1,-2),
设平面PBC的法向量
=(x,y,z),
则
,
取z=1,得
=(1,2,1),
又平面PBA的法向量
=(1,0,0),
∴cos<
,
>=
=
.
∴二面角C-PB-A的余弦值为
.
| PA |
| AB |
| PA |
| AC |
| AB |
| AC |
| PA |
| AC |
| AB |
∴PA⊥AB,PA⊥AC,AB⊥AC,PA=AC=2AB,
∴PA⊥平面ABC,∴PA⊥AB,

∴AB⊥平面PAC,∴AB⊥PC,
∵M为棱PC的中点,∴AM⊥PC,
又AM∩AB=A,∴PC⊥平面MAB.
(Ⅱ)解:以A为原点,AC为x轴,AB为y轴,AP为z轴,
建立空间直角坐标系,
设PA=AC=2AB=2,则C(2,0,0),P(0,0,2),
B(0,1,0),A(0,0,0),
| PC |
| PB |
设平面PBC的法向量
| n |
则
|
取z=1,得
| n |
又平面PBA的法向量
| m |
∴cos<
| n |
| m |
| 1 | ||
|
| ||
| 6 |
∴二面角C-PB-A的余弦值为
| ||
| 6 |
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
下列函数中,值域是(0,+∞)的函数是( )
A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=(
|
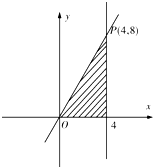 设不等式组
设不等式组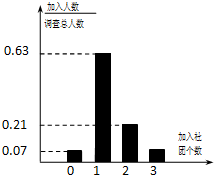 为了丰富学校课余文化生活,锻炼学生的综合能力,浏阳一中成立了多个学生社团,并鼓励学生参加社团活动或加入社团组织经过调研,若学生人均加入社团1~2个,则说明社团活动开展得有序.为此,学校规定学生加入的社团个数不能超过3个.社团文化节期间,校团委为了了解学生社团活动开展情况,随机发放并回收了100份调查问卷,并对各项指标进行了统计,其中学生参加社团的个数情况统计如图所示.
为了丰富学校课余文化生活,锻炼学生的综合能力,浏阳一中成立了多个学生社团,并鼓励学生参加社团活动或加入社团组织经过调研,若学生人均加入社团1~2个,则说明社团活动开展得有序.为此,学校规定学生加入的社团个数不能超过3个.社团文化节期间,校团委为了了解学生社团活动开展情况,随机发放并回收了100份调查问卷,并对各项指标进行了统计,其中学生参加社团的个数情况统计如图所示.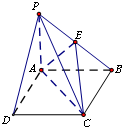 在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4
在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4