题目内容
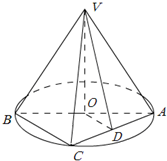如图，AB是圆O的直径，点C是弧AB的中点，点V是圆O所在平面外一点，D是AC的中点，已知AB=2，VA=VB=VC=2．（1）求证：OD∥平面VBC；
（2）求证：VO⊥平面ABC．
考点：直线与平面平行的判定,直线与平面垂直的判定
专题：空间位置关系与距离
分析：（1）先证明出OD∥BC，进而根据线面平行的判定定理证明出OD∥平面VBC．
（2）分别证明出VO⊥AB和OV⊥OC，最后根据线面垂直的判定定理证明出VO⊥平面ABC．
（2）分别证明出VO⊥AB和OV⊥OC，最后根据线面垂直的判定定理证明出VO⊥平面ABC．
解答：
证明：（1）∵O、D分别是AB和AC的中点，
∴OD∥BC．
又OD?BC，BC?BC，
∴OD∥平面VBC．
（2）∵VA=VB，O为AB中点，
∴VO⊥AB
连接OC，在△VOA，△VOC中OA=OC，VO=VO，VA=VC
∴△VOA≌△VOC，
∵∠AOV=90°
∴∠V0C=∠V0A=90°，即OV⊥OC，
∵AB∩OC=O，AB?平面ABC．OC?平面ABC，
∴VO⊥平面ABC．
证明：（1）∵O、D分别是AB和AC的中点，∴OD∥BC．
又OD?BC，BC?BC，
∴OD∥平面VBC．
（2）∵VA=VB，O为AB中点，
∴VO⊥AB
连接OC，在△VOA，△VOC中OA=OC，VO=VO，VA=VC
∴△VOA≌△VOC，
∵∠AOV=90°
∴∠V0C=∠V0A=90°，即OV⊥OC，
∵AB∩OC=O，AB?平面ABC．OC?平面ABC，
∴VO⊥平面ABC．
点评：本题主要考查了线面平行和线面垂直的判定定理的应用．考查了学生空间观察能力和逻辑推理能力．
练习册系列答案
相关题目
定义“D”：△f（x）=f（x+1）-f（x），△2f（x）=△[△f（x）]，△3f（x）=△[△2f（x）]，…，比如f（x）=x2，则有△f（x）=2x+1，△2f（x）=2，现已知f（x）=x2011，则△2012f（x）=（ ）
| A、1×2×3×…×2011 |
| B、1×2×3×…×2012 |
| C、2012 |
| D、0 |
