题目内容
“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是
.
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程);
(2)据此资料判断是否有95%的把握认为反感“中国式过马路”与性别有关?
| 男性 | 女性 | 合计 | |
| 反感 | 10 | ||
| 不反感 | 8 | ||
| 合计 | 30 |
| 8 |
| 15 |
(1)请将上面的列联表补充完整(在答题卷上直接填写结果,不需要写求解过程);
(2)据此资料判断是否有95%的把握认为反感“中国式过马路”与性别有关?
考点:独立性检验的应用
专题:计算题,概率与统计
分析:(1)根据在全部300人中随机抽取1人抽到中国式过马路的概率,做出中国式过马路的人数,进而做出男生的人数,填好表格;
(2)根据所给的公式,代入数据求出临界值,把求得的结果同临界值表进行比较,看出有多大的把握说明反感“中国式过马路”与性别是否有关.
(2)根据所给的公式,代入数据求出临界值,把求得的结果同临界值表进行比较,看出有多大的把握说明反感“中国式过马路”与性别是否有关.
解答:
解:(1)
…(6分)
(2)由已知数据得:Χ2=
≈1.158<3.841,
所以,没有95%的把握认为反感“中国式过马路”与性别无关. …(12分)
| 男性 | 女性 | 合计 | |
| 反感 | 10 | 6 | 16 |
| 不反感 | 6 | 8 | 14 |
| 合计 | 16 | 14 | 30 |
(2)由已知数据得:Χ2=
| 30(10×8-6×6)2 |
| 16×14×16×14 |
所以,没有95%的把握认为反感“中国式过马路”与性别无关. …(12分)
点评:本题考查了独立性检验,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
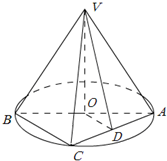 如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2. 一个三角形数表按如下方式构成(如图:其中项数n≥5):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:f(2,1)=f(1,1)+f(1,2);f(i,j)为数表中第i行的第j个数.
一个三角形数表按如下方式构成(如图:其中项数n≥5):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:f(2,1)=f(1,1)+f(1,2);f(i,j)为数表中第i行的第j个数.