题目内容
定义“D”:△f(x)=f(x+1)-f(x),△2f(x)=△[△f(x)],△3f(x)=△[△2f(x)],…,比如f(x)=x2,则有△f(x)=2x+1,△2f(x)=2,现已知f(x)=x2011,则△2012f(x)=( )
| A、1×2×3×…×2011 |
| B、1×2×3×…×2012 |
| C、2012 |
| D、0 |
考点:进行简单的合情推理
专题:推理和证明
分析:先考虑若f(x)=x,求出,△2f(x)=0;若f(x)=x2,得到△3f(x)=0;若f(x)=x3,得到△4f(x)=0;归纳出若f(x)=xn,则△n+1f(x)=0.从而得到△2012f(x)=0.
解答:
解:若f(x)=x,则△f(x)=f(x+1)-f(x)=1,△2f(x)=0;
若f(x)=x2,则△f(x)=2x+1,△2f(x)=2,△3f(x)=0;
若f(x)=x3,则△f(x)=3x2+3x+1,△2f(x)=6x+6,△3f(x)=6,△4f(x)=0;
…
若f(x)=xn,则△n+1f(x)=0.
∴若f(x)=x2011,则△2012f(x)=0.
故选D.
若f(x)=x2,则△f(x)=2x+1,△2f(x)=2,△3f(x)=0;
若f(x)=x3,则△f(x)=3x2+3x+1,△2f(x)=6x+6,△3f(x)=6,△4f(x)=0;
…
若f(x)=xn,则△n+1f(x)=0.
∴若f(x)=x2011,则△2012f(x)=0.
故选D.
点评:本题主要考查简单的合情推理:归纳推理,先通过几个特殊的情况,从而归纳出一般情况.

练习册系列答案
相关题目
算法语句如图所示:这个算法是用于( )


| A、计算3×10的值 |
| B、计算39的值 |
| C、计算1×2×3×…×10的值 |
| D、计算310的值 |
已知-
<θ<
,且sinθ+cosθ=
,则tanθ的值为( )
| π |
| 2 |
| π |
| 2 |
| ||
| 5 |
| A、-3 | ||
B、3或
| ||
C、-
| ||
D、-3或-
|
已知命题p:?x∈R,2x2-1≤0,则¬P:( )
| A、?x∈R,2x2-1≤0 |
| B、?x∈R,2x2-1>0 |
| C、?x∈R,2x2-1≤0 |
| D、?x∈R,2x2-1>0 |
设X为随机变量,X~B(n,
),若随机变量X的方差D(X)=1,则P(X=2)等于( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
圆(x-3)2+y2=4与圆x2+(y-4)2=16的位置关系为( )
| A、内切 | B、外切 | C、相交 | D、相离 |
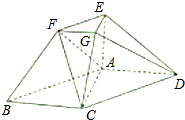 在如图所示的几何体中,ABCD为平行四边形,∠ACB=
在如图所示的几何体中,ABCD为平行四边形,∠ACB=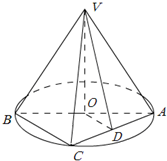 如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.