题目内容
将编号为A1,A2,…,A16的16名高一学生编为两组(甲组、乙组),他们在某次数学测验中的得分纪录如下:
(Ⅰ)将得分在对应区间内的人数填入相应的空格:
(Ⅱ)写出甲组学生得分数据的中位数;
(Ⅲ)从得分在区间[80,90)内的学生中随机抽取2人,
(i)用学生的编号列出所有可能的抽取结果;
(ii)求这2人均来自同一组的概率.
| 甲组 | 编号 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 |
| 得分 | 78 | 85 | 92 | 67 | 55 | 86 | 78 | 95 | |
| 乙组 | 编号 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 |
| 得分 | 87 | 86 | 75 | 63 | 92 | 82 | 71 | 68 |
| 区间 | [70,80) | [80,90) | [90,100] |
| 人数 |
(Ⅲ)从得分在区间[80,90)内的学生中随机抽取2人,
(i)用学生的编号列出所有可能的抽取结果;
(ii)求这2人均来自同一组的概率.
考点:古典概型及其概率计算公式,众数、中位数、平均数
专题:应用题,概率与统计
分析:(Ⅰ)由已知表格可得对应区间内的人数;
(Ⅱ)由中位数的意义可求;
(Ⅲ)(i)由已知数据可求;(ii)根据古典概型的概率计算公式可求;
(Ⅱ)由中位数的意义可求;
(Ⅲ)(i)由已知数据可求;(ii)根据古典概型的概率计算公式可求;
解答:
(Ⅰ)
(Ⅱ)由表格知中位数:
=81.5;
(Ⅲ)(i)所有可能的结果为:{A2,A6},{A2,A9},{A2,A10},{A2,A14},
{A6,A9},{A6,A10},{A6,A14},{A9,A10},{A9,A14},{A10,A14).
(ii)设“这2人均来自同一个组”为事件A,所有可能的结果有10种,2人均来自同一个组的结果有4种.
所以,这2人均来自同一个组的概率为P(A)=
=
.
| 区间 | [70,80) | [80,90) | [90,100] |
| 人数 | 4 | 5 | 3 |
| 78+85 |
| 2 |
(Ⅲ)(i)所有可能的结果为:{A2,A6},{A2,A9},{A2,A10},{A2,A14},
{A6,A9},{A6,A10},{A6,A14},{A9,A10},{A9,A14},{A10,A14).
(ii)设“这2人均来自同一个组”为事件A,所有可能的结果有10种,2人均来自同一个组的结果有4种.
所以,这2人均来自同一个组的概率为P(A)=
| 4 |
| 10 |
| 2 |
| 5 |
点评:该题考查古典概型及其概率计算公式和中位数的意义,属基础题.

练习册系列答案
相关题目
已知命题p:?x∈R,2x2-1≤0,则¬P:( )
| A、?x∈R,2x2-1≤0 |
| B、?x∈R,2x2-1>0 |
| C、?x∈R,2x2-1≤0 |
| D、?x∈R,2x2-1>0 |
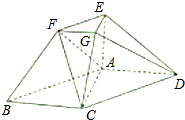 在如图所示的几何体中,ABCD为平行四边形,∠ACB=
在如图所示的几何体中,ABCD为平行四边形,∠ACB=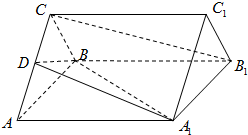 如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是
如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是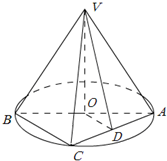 如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2. 一个三角形数表按如下方式构成(如图:其中项数n≥5):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:f(2,1)=f(1,1)+f(1,2);f(i,j)为数表中第i行的第j个数.
一个三角形数表按如下方式构成(如图:其中项数n≥5):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:f(2,1)=f(1,1)+f(1,2);f(i,j)为数表中第i行的第j个数.