题目内容
下列函数,自变量x如何变化,函数值可以无穷小:
(1)y=
;
(2)y=2x-1.
(1)y=
| 1 |
| x-1 |
(2)y=2x-1.
考点:极限及其运算
专题:导数的概念及应用
分析:无穷小就是极限为0,故本题是求极限为0时自变量的取值.
解答:
解:(1)∵
=0,
∴x趋向于正穷大时,y=
的函数值可以无穷小.
(2)∵
(2x-1)=0,
∴x趋向于
时,y=2x-1的函数值可以无穷小.
| lim |
| x→+∞ |
| 1 |
| x-1 |
∴x趋向于正穷大时,y=
| 1 |
| x-1 |
(2)∵
| lim | ||
x→
|
∴x趋向于
| 1 |
| 2 |
点评:本题考查极限为0时自变量的取值,解题时要认真审题,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知-
<θ<
,且sinθ+cosθ=
,则tanθ的值为( )
| π |
| 2 |
| π |
| 2 |
| ||
| 5 |
| A、-3 | ||
B、3或
| ||
C、-
| ||
D、-3或-
|
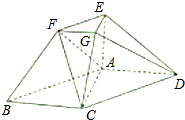 在如图所示的几何体中,ABCD为平行四边形,∠ACB=
在如图所示的几何体中,ABCD为平行四边形,∠ACB=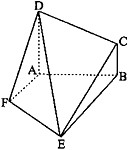 如图,四边形ABCD和ABEF都是直角梯形,AD∥BC,AF∥BE,∠DAB=∠FAB=90°,且平面ABCD⊥平面ABEF,DA=AB=BE=2,BC=1.
如图,四边形ABCD和ABEF都是直角梯形,AD∥BC,AF∥BE,∠DAB=∠FAB=90°,且平面ABCD⊥平面ABEF,DA=AB=BE=2,BC=1.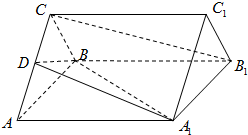 如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是
如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是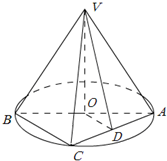 如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.