题目内容
某同学在研究性学习中,收集到某制药厂车间工人数(单位:十人)与药品产量(单位:万盒)的数据如表所示:
(1)请画出如表数据的散点图;
(2)参考公式,根据表格提供的数据,用最小二乘法求出y关于x的线性回归方程y=
x+
;(参考数据
i2=30,
xiyi=50)
(3)试根据(2)求出的线性回归方程,预测该制药厂车间工人数为45时,药品产量是多少?
| 工人数:x(单位:十人) | 1 | 2 | 3 | 4 |
| 药品产量:y(单位:万盒) | 3 | 4 | 5 | 6 |
(2)参考公式,根据表格提供的数据,用最小二乘法求出y关于x的线性回归方程y=
 |
| b |
 |
| a |
| 4 |
 |
| i=1 |
| 4 |
 |
| i=1 |
(3)试根据(2)求出的线性回归方程,预测该制药厂车间工人数为45时,药品产量是多少?
考点:线性回归方程
专题:应用题,概率与统计
分析:(1)根据表中所给的数据,得到点的坐标,在平面直角坐标系中画出散点图.
(2)先求出横标和纵标的平均数,得到这组数据的样本中心点,利用最小二乘法求出线性回归方程的系数,代入样本中心点求出a的值,写出线性回归方程.
(3)由回归直线方程,计算当x=4.5时,可求对应的药品产量.
(2)先求出横标和纵标的平均数,得到这组数据的样本中心点,利用最小二乘法求出线性回归方程的系数,代入样本中心点求出a的值,写出线性回归方程.
(3)由回归直线方程,计算当x=4.5时,可求对应的药品产量.
解答:
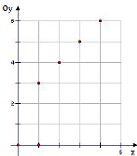 解:(1)散点图如图;
解:(1)散点图如图;
(2)由题意知:
=
(1+2+3+4)=2.5,
=
(3+4+5+6)=4.5,
=
=1,a=4.5-2.5=2,
∴要求的线性回归方程是y=x+2,
(3)当x=4.5时,y=6.5.
 解:(1)散点图如图;
解:(1)散点图如图;(2)由题意知:
. |
| x |
| 1 |
| 4 |
. |
| y |
| 1 |
| 4 |
| ∧ |
| b |
| 50-4•2.5•4.5 |
| 30-4•2.52 |
∴要求的线性回归方程是y=x+2,
(3)当x=4.5时,y=6.5.
点评:本题考查散点图,考查线性回归方程的求法,考查利用线性回归方程进行预测,属于基础题.

练习册系列答案
相关题目
设X为随机变量,X~B(n,
),若随机变量X的方差D(X)=1,则P(X=2)等于( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
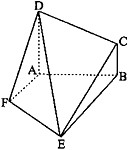 如图,四边形ABCD和ABEF都是直角梯形,AD∥BC,AF∥BE,∠DAB=∠FAB=90°,且平面ABCD⊥平面ABEF,DA=AB=BE=2,BC=1.
如图,四边形ABCD和ABEF都是直角梯形,AD∥BC,AF∥BE,∠DAB=∠FAB=90°,且平面ABCD⊥平面ABEF,DA=AB=BE=2,BC=1.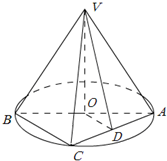 如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.