题目内容
已知a，b，c∈R，a2+b2+c2=1．
（Ⅰ）求证：|a+b+c|≤
；
（Ⅱ）若不等式|x-1|+|x+1|≥（a-b+c）2对一切实数a，b，c恒成立，求实数x的取值范围．
（Ⅰ）求证：|a+b+c|≤
| 3 |
（Ⅱ）若不等式|x-1|+|x+1|≥（a-b+c）2对一切实数a，b，c恒成立，求实数x的取值范围．
考点：二维形式的柯西不等式,函数恒成立问题
专题：选作题,不等式
分析：（Ⅰ）利用柯西不等式得，（a+b+c）2≤（12+12+12）（a2+b2+c2）=3；
（Ⅱ）同理，（a-b+c）2≤[12+（-1）2+12]（a2+b2+c2）=3，问题等价于|x-1|+|x+1|≥3．
（Ⅱ）同理，（a-b+c）2≤[12+（-1）2+12]（a2+b2+c2）=3，问题等价于|x-1|+|x+1|≥3．
解答：
解：（Ⅰ）由柯西不等式得，（a+b+c）2≤（12+12+12）（a2+b2+c2）=3
所以-
≤a+b+c≤
所以：|a+b+c|≤
； …（5分）
（Ⅱ）同理，（a-b+c）2≤[12+（-1）2+12]（a2+b2+c2）=3 …（7分）
若不等式|x-1|+|x+1|≥（a-b+c）2对一切实数a，b，c恒成立，
则|x-1|+|x+1|≥3，解集为（-∞，-
]∪[
，+∞） …（10分）
所以-
| 3 |
| 3 |
所以：|a+b+c|≤
| 3 |
（Ⅱ）同理，（a-b+c）2≤[12+（-1）2+12]（a2+b2+c2）=3 …（7分）
若不等式|x-1|+|x+1|≥（a-b+c）2对一切实数a，b，c恒成立，
则|x-1|+|x+1|≥3，解集为（-∞，-
| 3 |
| 2 |
| 3 |
| 2 |
点评：本题考查柯西不等式，考查恒成立问题，正确运用柯西不等式是关键．
练习册系列答案
高效智能课时作业系列答案
相关题目
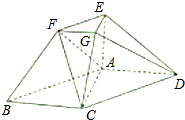在如图所示的几何体中，ABCD为平行四边形，∠ACB=
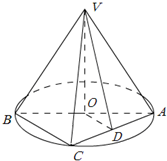如图，AB是圆O的直径，点C是弧AB的中点，点V是圆O所在平面外一点，D是AC的中点，已知AB=2，VA=VB=VC=2．
一个三角形数表按如下方式构成（如图：其中项数n≥5）：第一行是以4为首项，4为公差的等差数列，从第二行起，每一个数是其肩上两个数的和，例如：f（2，1）=f（1，1）+f（1，2）；f（i，j）为数表中第i行的第j个数．