题目内容
已知f(x)=(1+mx)(1-x)n=a0+a1x+a2x2+…+an+1xn+1(m∈R,n∈N+),其中a1=a2=-3.
(Ⅰ)求m,n的值;
(Ⅱ)求f(x)展开式中所有含x的奇次幂的项的系数和.
(Ⅰ)求m,n的值;
(Ⅱ)求f(x)展开式中所有含x的奇次幂的项的系数和.
考点:二项式系数的性质
专题:二项式定理
分析:(Ⅰ)由题意根据二项式定理可得,a1=-
+m=-3,a2=
-m
=-3,由此求得m、n的值.
(Ⅱ)求出 f(1)=a0+a1+a2+…+a7=0,f(-1)=a0-a1+a2-a3+…-a7=-128,即可求得a1+a3+a5+a7的值.
| C | 1 n |
| C | 2 n |
| C | 1 n |
(Ⅱ)求出 f(1)=a0+a1+a2+…+a7=0,f(-1)=a0-a1+a2-a3+…-a7=-128,即可求得a1+a3+a5+a7的值.
解答:
解:(Ⅰ)由题意根据二项式定理可得,a1=-
+m=m-n a2=
-m
-
-mn,
依题设,有
,解得
.
(Ⅱ)由(Ⅰ)可知 f(x)=(1+3x)(1-x)6=a0+a1x+a2x2+…+a7x7,
∴f(1)=a0+a1+a2+…+a7=0,f(-1)=a0-a1+a2-a3+…-a7=-128.
∴展开式中所有含x的奇次幂的项的系数和 a1+a3+a5+a7=64.
| C | 1 n |
| C | 2 n |
| C | 1 n |
| n(n-1) |
| 2 |
依题设,有
|
|
(Ⅱ)由(Ⅰ)可知 f(x)=(1+3x)(1-x)6=a0+a1x+a2x2+…+a7x7,
∴f(1)=a0+a1+a2+…+a7=0,f(-1)=a0-a1+a2-a3+…-a7=-128.
∴展开式中所有含x的奇次幂的项的系数和 a1+a3+a5+a7=64.
点评:本题主要考查二项式定理、赋值法等基础知识,考查观察能力、运算求解能力、推理能力和函数与方程思想,属于基础题.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
圆(x-3)2+y2=4与圆x2+(y-4)2=16的位置关系为( )
| A、内切 | B、外切 | C、相交 | D、相离 |
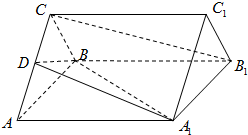 如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是
如图,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是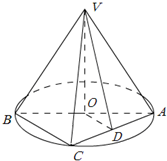 如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2.
如图,AB是圆O的直径,点C是弧AB的中点,点V是圆O所在平面外一点,D是AC的中点,已知AB=2,VA=VB=VC=2. 一个三角形数表按如下方式构成(如图:其中项数n≥5):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:f(2,1)=f(1,1)+f(1,2);f(i,j)为数表中第i行的第j个数.
一个三角形数表按如下方式构成(如图:其中项数n≥5):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:f(2,1)=f(1,1)+f(1,2);f(i,j)为数表中第i行的第j个数.