题目内容
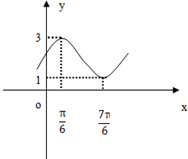 如图所示,为函数f(x)=Asin(ωx+ϕ)+b图象的一部分.根据图象:
如图所示,为函数f(x)=Asin(ωx+ϕ)+b图象的一部分.根据图象:(1)求出函数f(x)的解析式;
(2)写出f(x)的单调递增区间.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,复合三角函数的单调性
专题:三角函数的图像与性质
分析:(1)由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,从而求得函数的解析式.
(2)令2kπ-
≤x+
≤2kπ+
,k∈z,求得x的范围,可得f(x)的单调递增区间.
(2)令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解答:
解:(1)如图所示,∵
=
-
=π,∴t=2π,ω=1,
A=
=1,b=2.
当 x=
时,
+φ=
,∴φ=
,∴f(x)=sin(x+
)+2.
(2)令2kπ-
≤x+
≤2kπ+
,k∈z,求得2kπ-
≤x≤2kπ+
,
∴f(x)的单调递增区间是[2kπ-
,2kπ+
](k∈Z).
| T |
| 2 |
| 7π |
| 6 |
| π |
| 6 |
A=
| 3-1 |
| 2 |
当 x=
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
(2)令2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
| π |
| 6 |
∴f(x)的单调递增区间是[2kπ-
| 5π |
| 6 |
| π |
| 6 |
点评:本题主要考查利用y=Asin(ωx+φ)的图象特征,由函数y=Asin(ωx+φ)的部分图象求解析式,求正弦函数的增区间,由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,属于中档题.

练习册系列答案
相关题目
若m,n是两条不同的直线,α,β,γ是三个不同的平面,则下面命题正确的是( )
| A、若m⊆β,α⊥β,则m⊥α |
| B、若α∩γ=m,β∩γ=n,则α∥β |
| C、若m⊥β,m∥α,则α⊥β |
| D、若α⊥β,α⊥γ,则β⊥γ |
设z=
+(1-i)2,则(1+x)4(1+zx)3展开式中x5项的系数是( )
| 1+i |
| 1-i |
| A、-2-3i |
| B、-12+3i |
| C、1+21i |
| D、-35i |

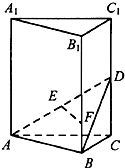 如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF
如图,在直三棱柱ABC-A1B1C1中,D、E分别为CC1、AD的中点,F为BB1上的点,且B1F=3BF