题目内容
如图，正方体的底面与正四面体的底面在同一平面α上，且AB∥CD，正方体的六个面所在的平面与直线CE，EF相交的平面个数分别记为m，n，那么m+n= ．
考点：空间中直线与平面之间的位置关系
专题：综合题,空间位置关系与距离
分析：判断CE与EF与正方体表面的关系，即可推出正方体的六个面所在的平面与直线CE，EF相交的平面个数分别记为m，n，求出m+n的值．
解答：
解：由题意可知直线CE与正方体的上底面平行在正方体的下底面上，与正方体的四个侧面不平行，所以m=4，
直线EF与正方体的左右两个侧面平行，与正方体的上下底面相交，前后侧面相交，所以n=4，所以m+n=8．
故答案为：8．
直线EF与正方体的左右两个侧面平行，与正方体的上下底面相交，前后侧面相交，所以n=4，所以m+n=8．
故答案为：8．
点评：本题考查直线与平面的位置关系，基本知识的应用，考查空间想象能力．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
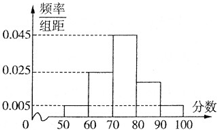某学校举行课外综合知识比赛，随机抽取400名同学的成绩，成绩全部在50分至100分之间，将成绩按如下方式分成5组：第一组，成绩大于等于50分且小于60分；第二组，成绩大于等于60分且小于70分…第五组，成绩大于等于90分且小于等于100分，据此绘制了如图所示的频率分布直方图．则400名同学中成绩优秀（大于等于80分）的学生有
（理）y=sin3x+cos2x-sinx的最大值（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
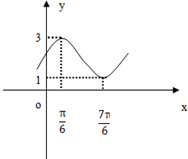如图所示，为函数f（x）=Asin（ωx+ϕ）+b图象的一部分．根据图象：