题目内容
若m,n是两条不同的直线,α,β,γ是三个不同的平面,则下面命题正确的是( )
| A、若m⊆β,α⊥β,则m⊥α |
| B、若α∩γ=m,β∩γ=n,则α∥β |
| C、若m⊥β,m∥α,则α⊥β |
| D、若α⊥β,α⊥γ,则β⊥γ |
考点:空间中直线与平面之间的位置关系
专题:综合题,空间位置关系与距离
分析:A,B,D列举所有可能,即可判断;C,由面面垂直的判定定理,我们易得正确;
解答:
解:对于A,若m⊆β,α⊥β,则m⊥α,也有可能平行、相交,故不正确;
对于B,若α∩γ=m,β∩γ=n,则α∥β或α、β相交,故不正确;
对于C,设经过m的平面与α相交于a,则m∥a,因为m⊥β,所以a⊥β,由面面垂直的判定定理,我们易得正确;
对于D,α⊥β,α⊥γ,则β与γ平行、相交都有可能,故不正确.
故选:C.
对于B,若α∩γ=m,β∩γ=n,则α∥β或α、β相交,故不正确;
对于C,设经过m的平面与α相交于a,则m∥a,因为m⊥β,所以a⊥β,由面面垂直的判定定理,我们易得正确;
对于D,α⊥β,α⊥γ,则β与γ平行、相交都有可能,故不正确.
故选:C.
点评:要判断空间中直线与平面的位置关系,有良好的空间想像能力,熟练掌握空间中直线与直线、直线与平面、平面与平面平行或垂直的判定定理及性质定理,并能利用教室、三棱锥、长方体等实例举出满足条件的例子或反例是解决问题的重要条件.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
(理)y=sin3x+cos2x-sinx的最大值( )
A、
| ||
B、
| ||
C、
| ||
D、
|
如图,该程序运行后输出的结果为( )


| A、20 | B、32 | C、38 | D、40 |
执行如图所示的程序框图,若输入的p=0.8,则输出的n为( )


| A、4 | B、5 | C、6 | D、3 |
已知g(x)=ax+a,f(x)=
,对?x1∈[-2,2],?x2∈[-2,2],使g(x1)=f(x2)成立,则a的取值范围是( )
|
| A、[-1,+∞) |
| B、[-1,1] |
| C、(0,1] |
| D、(-∞,1] |
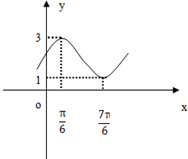 如图所示,为函数f(x)=Asin(ωx+ϕ)+b图象的一部分.根据图象:
如图所示,为函数f(x)=Asin(ωx+ϕ)+b图象的一部分.根据图象: