题目内容
已知函数f（x）=x2+xsinx+cosx．
（1）求f（x）的最小值；
（2）若曲线y=f（x）在点（a，f（a））处与直线y=b相切，求a与b的值．
（1）求f（x）的最小值；
（2）若曲线y=f（x）在点（a，f（a））处与直线y=b相切，求a与b的值．
考点：导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题：综合题,导数的综合应用
分析：（1）由已知中函数的解析式，求导后判断函数的单调性，进而可得f（x）的最小值；
（2）若曲线y=f（x）在点（a，f（a））处与直线y=b相切，则f′（a）=0，b=f（a），进而可得a与b的值．
（2）若曲线y=f（x）在点（a，f（a））处与直线y=b相切，则f′（a）=0，b=f（a），进而可得a与b的值．
解答：
解：（1）由f（x）=x2+xsinx+cosx，
得f′（x）=2x+sinx+xcosx-sinx=x（2+cosx）．
令f′（x）=0，得x=0．
列表如下：
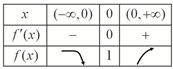
∴函数f（x）在区间（-∞，0）上单调递减，
在区间（0，+∞）上单调递增，
∴f（0）=1是f（x）的最小值；
（2）∵曲线y=f（x）在点（a，f（a））处与直线y=b相切，
∴f′（a）=a（2+cosa）=0，b=f（a），
解得a=0，b=f（0）=1．
得f′（x）=2x+sinx+xcosx-sinx=x（2+cosx）．
令f′（x）=0，得x=0．
列表如下：
∴函数f（x）在区间（-∞，0）上单调递减，
在区间（0，+∞）上单调递增，
∴f（0）=1是f（x）的最小值；
（2）∵曲线y=f（x）在点（a，f（a））处与直线y=b相切，
∴f′（a）=a（2+cosa）=0，b=f（a），
解得a=0，b=f（0）=1．
点评：本题考查的知识点是导数在最大值、最小值问题中的应用，导数法研究曲线的切线，是导数较为综合的应用，难度中档．
练习册系列答案
相关题目
已知g（x）=ax+a，f（x）=
，对?x1∈[-2，2]，?x2∈[-2，2]，使g（x1）=f（x2）成立，则a的取值范围是（ ）
|
| A、[-1，+∞） |
| B、[-1，1] |
| C、（0，1] |
| D、（-∞，1] |
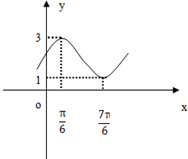如图所示，为函数f（x）=Asin（ωx+ϕ）+b图象的一部分．根据图象：