题目内容
设z=
+(1-i)2,则(1+x)4(1+zx)3展开式中x5项的系数是( )
| 1+i |
| 1-i |
| A、-2-3i |
| B、-12+3i |
| C、1+21i |
| D、-35i |
考点:复数代数形式的混合运算
专题:数系的扩充和复数,二项式定理
分析:由复数代数形式的混合运算化简复数z,代入(1+x)4(1+zx)3后由二项式的项的系数的运算性质列式求解展开式中x5项的系数.
解答:
解:∵z=
+(1-i)2=
-2i=
-2i=-i.
∴(1+x)4(1+zx)3=(1+x)4(1-ix)3,
展开式中x5项的系数是
•(-i)+
•
•i2+
•
•(-i)3=-12+3i.
故选:B.
| 1+i |
| 1-i |
| (1+i)2 |
| (1-i)(1+i) |
| 2i |
| 2 |
∴(1+x)4(1+zx)3=(1+x)4(1-ix)3,
展开式中x5项的系数是
| C | 4 4 |
| C | 1 3 |
| C | 3 4 |
| C | 2 3 |
| C | 2 4 |
| C | 3 3 |
故选:B.
点评:本题考查了复数代数形式的混合运算,考查了二项式系数的运算性质,是中档题.

练习册系列答案
相关题目
(理)y=sin3x+cos2x-sinx的最大值( )
A、
| ||
B、
| ||
C、
| ||
D、
|
执行如图所示的程序框图,若输入的p=0.8,则输出的n为( )


| A、4 | B、5 | C、6 | D、3 |
已知g(x)=ax+a,f(x)=
,对?x1∈[-2,2],?x2∈[-2,2],使g(x1)=f(x2)成立,则a的取值范围是( )
|
| A、[-1,+∞) |
| B、[-1,1] |
| C、(0,1] |
| D、(-∞,1] |
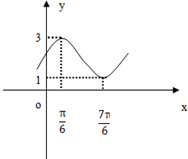 如图所示,为函数f(x)=Asin(ωx+ϕ)+b图象的一部分.根据图象:
如图所示,为函数f(x)=Asin(ωx+ϕ)+b图象的一部分.根据图象: