题目内容
已知定义在(0,+∞)上的函数f(x)对任意的x,y>0,均有f(xy)=f(x)•f(y),且当x>1时,f(x)<1,f(3)=
(1)求证f(x)>0;
(2)求证f(x)在(0,+∞)上单调递减;
(3)若f(m)=9,求m的值.
| 1 |
| 9 |
(1)求证f(x)>0;
(2)求证f(x)在(0,+∞)上单调递减;
(3)若f(m)=9,求m的值.
考点:抽象函数及其应用
专题:证明题,函数的性质及应用
分析:(1)运用赋值法,根据条件f(xy)=f(x)•f(y)将x,y换为
,舍去f(
)=0,即得f(x)>0;
(2)运用函数的单调性的定义,令0<x1<x2,则
>1,根据x>1时,f(x)<1,得到f(
)<1,再由f(xy)=f(x)•f(y)得
<1,再由(1)的结论得证;
(3)运用赋值法,令x=y=1,由条件求出f(1)=1,再令x=3,y=
,求出f(
)=9,从而得到f(m)=f(
),根据(2)的结论,即得m的值.
| x |
| x |
(2)运用函数的单调性的定义,令0<x1<x2,则
| x2 |
| x1 |
| x2 |
| x1 |
| f(x2) |
| f(x1) |
(3)运用赋值法,令x=y=1,由条件求出f(1)=1,再令x=3,y=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:
(1)证明:∵对任意的x,y>0,均有f(xy)=f(x)•f(y),
∴f(x)=f(
)•f(
)=f2(
),
若f(
)=0,则f(x)=0,这与f(3)>0矛盾,
∴f(x)>0成立;
(2)证明:令0<x1<x2,则
>1,
∵x>1时,f(x)<1,
∴f(
)<1,
∵f(xy)=f(x)•f(y),
∴f(x)=
,
∴f(
)=
<1,
由(1)得:f(x2)<f(x1),
∴由函数的单调性的定义得:
f(x)在(0,+∞)上单调递减;
(3)解:令x=y=1,则f(1)=f2(1),
即f(1)=1或f(1)=0(舍去),
又f(3)=
,
∴f(
)=
=
=9,
∵f(m)=9,
∴f(m)=f(
),
∵f(x)在(0,+∞)上单调递减,
∴m=
.
∴f(x)=f(
| x |
| x |
| x |
若f(
| x |
∴f(x)>0成立;
(2)证明:令0<x1<x2,则
| x2 |
| x1 |
∵x>1时,f(x)<1,
∴f(
| x2 |
| x1 |
∵f(xy)=f(x)•f(y),
∴f(x)=
| f(xy) |
| f(y) |
∴f(
| x2 |
| x1 |
| f(x2) |
| f(x1) |
由(1)得:f(x2)<f(x1),
∴由函数的单调性的定义得:
f(x)在(0,+∞)上单调递减;
(3)解:令x=y=1,则f(1)=f2(1),
即f(1)=1或f(1)=0(舍去),
又f(3)=
| 1 |
| 9 |
∴f(
| 1 |
| 3 |
| f(1) |
| f(3) |
| 1 | ||
|
∵f(m)=9,
∴f(m)=f(
| 1 |
| 3 |
∵f(x)在(0,+∞)上单调递减,
∴m=
| 1 |
| 3 |
点评:本题主要考查函数的单调性的证明和运用,注意定义域的应用,同时考查赋值法在解决抽象函数问题时的灵活运用,注意条件的反复运用和灵活运用.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
(理)y=sin3x+cos2x-sinx的最大值( )
A、
| ||
B、
| ||
C、
| ||
D、
|
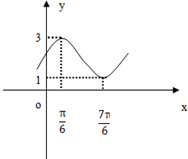 如图所示,为函数f(x)=Asin(ωx+ϕ)+b图象的一部分.根据图象:
如图所示,为函数f(x)=Asin(ωx+ϕ)+b图象的一部分.根据图象: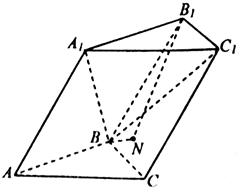 如图,三棱柱ABC-A1B1C1中,△ABC是正三角形,AA1=AB=2,平面ACC1A1⊥平面ABC,∠A1AC=60°.
如图,三棱柱ABC-A1B1C1中,△ABC是正三角形,AA1=AB=2,平面ACC1A1⊥平面ABC,∠A1AC=60°.