题目内容
17.在平面内,点A,B,C分别在直线l1、l2、l3上,且l1∥l2∥l3(l2在l1与l3之间),l1与l2间距离为a,l2与l3之间距离为b,且$\overrightarrow{AB}$2=$\overrightarrow{AB}$•$\overrightarrow{AC}$,则△ABC的面积最小值为( )| A. | $\frac{a+b}{2}$ | B. | ab | C. | 2$\sqrt{ab}$ | D. | $\frac{{a}^{2}+{b}^{2}}{2}$ |
分析 由条件判断$\overrightarrow{AB}⊥\overrightarrow{CB}$,再作辅助线利用直角三角形中的边角关系求出AB、AC的长,可得S△ABC 的解析式,再根据正弦函数的值域,求得它的最小值.
解答 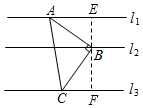 解:△ABC中,由$\overrightarrow{AB}$2=$\overrightarrow{AB}$•$\overrightarrow{AC}$,可得$\overrightarrow{AB}$•($\overrightarrow{AB}-\overrightarrow{AC}$)=$\overrightarrow{AB}•\overrightarrow{CB}$=0,∴$\overrightarrow{AB}⊥\overrightarrow{CB}$.
解:△ABC中,由$\overrightarrow{AB}$2=$\overrightarrow{AB}$•$\overrightarrow{AC}$,可得$\overrightarrow{AB}$•($\overrightarrow{AB}-\overrightarrow{AC}$)=$\overrightarrow{AB}•\overrightarrow{CB}$=0,∴$\overrightarrow{AB}⊥\overrightarrow{CB}$.
过点B作EF⊥l2,交l1于E,交l3于F,如图所示,
∵EF⊥l2,l1∥l2∥l3,∴EF⊥l1⊥l3,
∴∠ABE+∠EAB=90°,∠AEB=∠BFC=90°.
又∵∠ABC=90°,∴∠ABE+∠FBC=90°,∴∠EAB=∠FBC=θ,且θ为锐角.
在△ABE和△BCF中,∵BE=a,BF=b,∴AB=$\frac{BE}{sinθ}$=$\frac{a}{sinθ}$,BC=$\frac{BF}{cosθ}$=$\frac{b}{cosθ}$.
∴S△ABC=$\frac{1}{2}$AB•BC=$\frac{1}{2}$•$\frac{a}{sinθ}•\frac{b}{cosθ}$=$\frac{ab}{sin2θ}$,故当θ=$\frac{π}{4}$时,S△ABC 取得最小值为ab,
故选:B.
点评 本题主要考查了两个向量的数量积的运算、两个向量垂直的判定,勾股定理、平行线之间的距离,解题的关键是作辅助线,求出AB和 AC的值,属于中档题.

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
 如图是60名学生参加数学竞赛的成绩(均为整数)的频率分布直方图,估计这次数学竞赛的及格率是( )
如图是60名学生参加数学竞赛的成绩(均为整数)的频率分布直方图,估计这次数学竞赛的及格率是( )| A. | 75% | B. | 25% | C. | 15% | D. | 40% |
| A. | (-∞,0) | B. | (0,1) | C. | (1,+∞) | D. | (-∞,0)∪(1,+∞) |
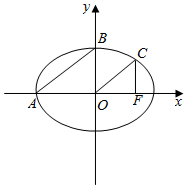 如图,A,B为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点,过椭圆的右焦点F作x轴的垂线,与其交于点C,若AB∥OC(O为坐标原点),则直线AB的斜率为$\frac{\sqrt{2}}{2}$.
如图,A,B为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点,过椭圆的右焦点F作x轴的垂线,与其交于点C,若AB∥OC(O为坐标原点),则直线AB的斜率为$\frac{\sqrt{2}}{2}$.