题目内容
5.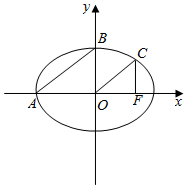 如图,A,B为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点,过椭圆的右焦点F作x轴的垂线,与其交于点C,若AB∥OC(O为坐标原点),则直线AB的斜率为$\frac{\sqrt{2}}{2}$.
如图,A,B为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点,过椭圆的右焦点F作x轴的垂线,与其交于点C,若AB∥OC(O为坐标原点),则直线AB的斜率为$\frac{\sqrt{2}}{2}$.
分析 由已知得C(c,$\frac{{b}^{2}}{a}$),A(-a,0),B(0,b),从而得到$\frac{b}{a}=\frac{\frac{{b}^{2}}{a}}{c}$,即b=c,由此能求出直线AB的斜率.
解答  解:∵A,B为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点
解:∵A,B为椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两个顶点
过椭圆的右焦点F作x轴的垂线,与其交于点C,AB∥OC(O为坐标原点),
∴C(c,$\frac{{b}^{2}}{a}$),A(-a,0),B(0,b),
∴$\frac{b}{a}=\frac{\frac{{b}^{2}}{a}}{c}$,∴bc=b2,∴b=c,
∴a2=b2+c2=2c2,
∴a=$\sqrt{2}c$=$\sqrt{2}b$,
∴直线AB的斜率k=$\frac{b}{a}=\frac{b}{\sqrt{2}b}$=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查直线方程的斜率的求法,是中档题,解题时要认真审题,注意椭圆性质的合理运用.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
13.若一个椭圆长轴的长度,短轴的长度和焦距依次成等差数列,则该椭圆的离心率是( )
| A. | e=-1 | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{1}{2}$ |
17.在平面内,点A,B,C分别在直线l1、l2、l3上,且l1∥l2∥l3(l2在l1与l3之间),l1与l2间距离为a,l2与l3之间距离为b,且$\overrightarrow{AB}$2=$\overrightarrow{AB}$•$\overrightarrow{AC}$,则△ABC的面积最小值为( )
| A. | $\frac{a+b}{2}$ | B. | ab | C. | 2$\sqrt{ab}$ | D. | $\frac{{a}^{2}+{b}^{2}}{2}$ |
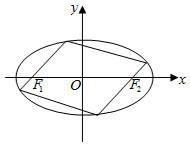 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其左、右焦点分别为F1(-c,0),F2(c,0)(c>0).
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),其左、右焦点分别为F1(-c,0),F2(c,0)(c>0).