题目内容
12. 如图是60名学生参加数学竞赛的成绩(均为整数)的频率分布直方图,估计这次数学竞赛的及格率是( )
如图是60名学生参加数学竞赛的成绩(均为整数)的频率分布直方图,估计这次数学竞赛的及格率是( )| A. | 75% | B. | 25% | C. | 15% | D. | 40% |
分析 先根据直方图中的各个矩形的面积代表了频率求出60分及以上的频率,从而估计总体中这次数学竞赛的及格率.
解答 解:大于或等于60分的共四组,它们是:
[59.5,69.5),[69.5,79.5),[79.5,89.5),[89.5,99.5).
分别计算出这四组的频率,
如[79.5,89.5)这一组的矩形的高为0.025
直方图中的各个矩形的面积代表了频率,则[79.5,89.5)这一组的频率=0.025×10=0.25
同样可得,60分及以上的频率=(0.015+0.03+0.025+0.005)×10=0.75
估计这次数学竞赛竞赛的及格率(大于或等于60分为及格)为75%,
故选:A.
点评 本题考查频率分布直方图的相关知识,直方图中的各个矩形的面积代表了频率,所以各个矩形面积之和为1,以及频数=样本容量×频率,属于基础题.

练习册系列答案
相关题目
17.在平面内,点A,B,C分别在直线l1、l2、l3上,且l1∥l2∥l3(l2在l1与l3之间),l1与l2间距离为a,l2与l3之间距离为b,且$\overrightarrow{AB}$2=$\overrightarrow{AB}$•$\overrightarrow{AC}$,则△ABC的面积最小值为( )
| A. | $\frac{a+b}{2}$ | B. | ab | C. | 2$\sqrt{ab}$ | D. | $\frac{{a}^{2}+{b}^{2}}{2}$ |
4.已知函数f(x)=sin(2x+φ)在x=$\frac{π}{6}$处取得极大值,则函数y=f($\frac{π}{4}$+x)的图象( )
| A. | 关于点($\frac{π}{6}$,0)对称 | B. | 关于点($\frac{π}{3}$,0)对称 | ||
| C. | 关于直线x=$\frac{π}{6}$对称 | D. | 关于直线x=$\frac{π}{3}$对称 |
 如图,已知⊙C1:(x+$\sqrt{6}$)2+y2=32及点C2($\sqrt{6}$,0),在⊙C1上任取一点P,连结C2P,作线段C2P的中垂线交直线C1P于点M.
如图,已知⊙C1:(x+$\sqrt{6}$)2+y2=32及点C2($\sqrt{6}$,0),在⊙C1上任取一点P,连结C2P,作线段C2P的中垂线交直线C1P于点M.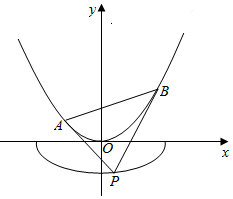 如图,已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)的离心率e=$\frac{\sqrt{6}}{3}$,且经过点G(1,-$\frac{\sqrt{6}}{3}$),曲线C2:x2=2y,过曲线C1上一点P作C2的两条切线,切点分别为A,B.
如图,已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≤0)的离心率e=$\frac{\sqrt{6}}{3}$,且经过点G(1,-$\frac{\sqrt{6}}{3}$),曲线C2:x2=2y,过曲线C1上一点P作C2的两条切线,切点分别为A,B.