题目内容
设f(x)=ax3+3x+2有极值,
(Ⅰ)求a的取值范围;
(Ⅱ)求极大值点和极小值点.
(Ⅰ)求a的取值范围;
(Ⅱ)求极大值点和极小值点.
考点:函数在某点取得极值的条件
专题:计算题,导数的概念及应用
分析:(Ⅰ)由f(x)=ax3+x+1有极值,导数等于0一定有解,求出a的值,再验证当a在这个范围中时,f(x)=ax3+x+1有极值,则求出的a的范围就是f(x)=ax3+x+1有极值的充要条件.;
(Ⅱ)确定函数的单调性,即可求出极大值点和极小值点.
(Ⅱ)确定函数的单调性,即可求出极大值点和极小值点.
解答:
解:(Ⅰ)f(x)=ax3+3x+2的导数为f′(x)=3ax2+3,
若函数f(x)有极值,则f′(x)=0有两个不同的解,即3ax2+3=0有解,∴a<0
若a<0,则3ax2+1=0有解,即f′(x)=0有解,∴函数f(x)有极值.
∴函数f(x)=ax3+x+1有极值时,a<0
(Ⅱ)a<0时,3ax2+3=0,∴x=±
,
函数在(-∞,-
),(
,+∞)上单调递减,在(-
,
)上单调递增,
∴极大值点为
,极小值点为
.
若函数f(x)有极值,则f′(x)=0有两个不同的解,即3ax2+3=0有解,∴a<0
若a<0,则3ax2+1=0有解,即f′(x)=0有解,∴函数f(x)有极值.
∴函数f(x)=ax3+x+1有极值时,a<0
(Ⅱ)a<0时,3ax2+3=0,∴x=±
|
函数在(-∞,-
|
|
|
|
∴极大值点为
|
|
点评:本题主要考查了函数的导数与极值的关系,考查极值点,属于综合题.

练习册系列答案
相关题目
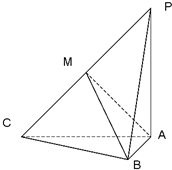 如图,三棱锥P-ABC中,
如图,三棱锥P-ABC中,