题目内容
已知点O是△ABC内的一点,∠AOB=150°,∠BOC=90°设
=
,
=
,
=
,且|
|=2,|
|=1,|
|=3,试用
和
表示
.
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
考点:向量在几何中的应用
专题:综合题,平面向量及应用
分析:以O为原点,OC,OB所在的直线为x轴和y轴建立如图所示的坐标系,求出A,B,C的坐标,利用平面向量基本定理,即可用
和
表示
.
| a |
| b |
| c |
解答:
 解:以O为原点,OC,OB所在的直线为x轴和y轴建立如图所示的坐标系.由OA=2,∠AOx=120°,
解:以O为原点,OC,OB所在的直线为x轴和y轴建立如图所示的坐标系.由OA=2,∠AOx=120°,
所以A(2cos120°,2sin120°),即A(-1,
),
易求B(0,-1),C(3,0),
设
=λ1
+λ2
,则
(-1,
)=λ1(0,-1)+λ2(3,0),
∴
,
∴λ1=-
,λ2=-
所以
=-3
-3
.
 解:以O为原点,OC,OB所在的直线为x轴和y轴建立如图所示的坐标系.由OA=2,∠AOx=120°,
解:以O为原点,OC,OB所在的直线为x轴和y轴建立如图所示的坐标系.由OA=2,∠AOx=120°,所以A(2cos120°,2sin120°),即A(-1,
| 3 |
易求B(0,-1),C(3,0),
设
| OA |
| OB |
| OC |
(-1,
| 3 |
∴
|
∴λ1=-
| 3 |
| 1 |
| 3 |
所以
| c |
| a |
| 3 |
| b |
点评:本题考查平面向量基本定理,考查方程组思想,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
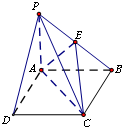 在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4
在四棱锥P-ABCD中,底面ABCD为边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4