题目内容
已知椭圆的左焦点为F,左右顶点分别为A、C,上顶点为B,O为原点,P为椭圆上任意一点,过F、B、C三点的圆的圆心坐标为(m,n).
(1)当m+n≤0时,求椭圆的离心率的取值范围;
(2)在(1)的条件下,椭圆的离心率最小时,若点D(b+1,0),(
+
)•
的最小值为
,求椭圆的方程.
(1)当m+n≤0时,求椭圆的离心率的取值范围;
(2)在(1)的条件下,椭圆的离心率最小时,若点D(b+1,0),(
| PF |
| OD |
| PO |
| 7 |
| 2 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意可得B(0,b),C(a,0),F(-c,0).设过F、B、C三点的圆的方程为x2+y2+ux+vy+s=0,把B,C,F三点坐标代入可得u=c-a,v=
,s=-ac.可得m=-
,n=-
,利用m+n≤0,即可得出;
(2)在(1)的条件下,椭圆的离心率最小时,e=
.可设椭圆的方程为
+
=1,即x2+2y2=2b2.设P(x,y),F(-b,0),则(
+
)•
=x2-x+y2=
(x-1)2+b2-
≥b2-
.
| ac-b2 |
| b |
| u |
| 2 |
| v |
| 2 |
(2)在(1)的条件下,椭圆的离心率最小时,e=
| ||
| 2 |
| x2 |
| 2b2 |
| y2 |
| b2 |
| PF |
| OD |
| PO |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)由题意可得B(0,b),C(a,0),F(-c,0).
设过F、B、C三点的圆的方程为x2+y2+ux+vy+s=0,
可得
,解得u=c-a,v=
,s=-ac.
∴m=-
=
,n=-
=
,
∵m+n≤0,∴
+
≤0,化为a2≤2c2,
∴e≥
,
又e<1.∴
≤e<1,
∴椭圆的离心率的取值范围是[
,1).
(2)在(1)的条件下,椭圆的离心率最小时,e=
.
可设椭圆的方程为
+
=1,即x2+2y2=2b2(b=c).
设P(x,y),F(-b,0),
则(
+
)•
=x2-x+y2=x2-x+b2-
x2=
(x-1)2+b2-
≥b2-
.
∴b2-
=
,解得b2=4,
∴椭圆的方程为
+
=1.
设过F、B、C三点的圆的方程为x2+y2+ux+vy+s=0,
可得
|
| ac-b2 |
| b |
∴m=-
| u |
| 2 |
| a-c |
| 2 |
| v |
| 2 |
| b2-ac |
| 2b |
∵m+n≤0,∴
| a-c |
| 2 |
| b2-ac |
| 2b |
∴e≥
| ||
| 2 |
又e<1.∴
| ||
| 2 |
∴椭圆的离心率的取值范围是[
| ||
| 2 |
(2)在(1)的条件下,椭圆的离心率最小时,e=
| ||
| 2 |
可设椭圆的方程为
| x2 |
| 2b2 |
| y2 |
| b2 |
设P(x,y),F(-b,0),
则(
| PF |
| OD |
| PO |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴b2-
| 1 |
| 2 |
| 7 |
| 2 |
∴椭圆的方程为
| x2 |
| 8 |
| y2 |
| 4 |
点评:本题考查了椭圆的标准方程及其性质、三角形的外接圆的方程、向量的坐标运算及其数量积运算、二次函数的单调性等基础知识与基本技能方法,考查了推理能力与计算能力.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
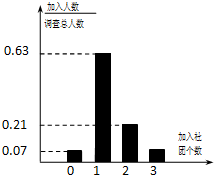 为了丰富学校课余文化生活,锻炼学生的综合能力,浏阳一中成立了多个学生社团,并鼓励学生参加社团活动或加入社团组织经过调研,若学生人均加入社团1~2个,则说明社团活动开展得有序.为此,学校规定学生加入的社团个数不能超过3个.社团文化节期间,校团委为了了解学生社团活动开展情况,随机发放并回收了100份调查问卷,并对各项指标进行了统计,其中学生参加社团的个数情况统计如图所示.
为了丰富学校课余文化生活,锻炼学生的综合能力,浏阳一中成立了多个学生社团,并鼓励学生参加社团活动或加入社团组织经过调研,若学生人均加入社团1~2个,则说明社团活动开展得有序.为此,学校规定学生加入的社团个数不能超过3个.社团文化节期间,校团委为了了解学生社团活动开展情况,随机发放并回收了100份调查问卷,并对各项指标进行了统计,其中学生参加社团的个数情况统计如图所示.