题目内容

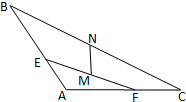如图，△ABC中，AB=AC=1，∠A=120°，E，F分别是边AB，AC上的点，且
AE
=m
AB
，
AF
=n
AC
，其中m，n∈（0，1），若EF，BC的中点分别为M，N，且m+n=1，则|
MN
|的最小值是（　　）
A、
1
2
B、
7
7
C、
1
4
D、
7
14
考点：平面向量数量积的运算
专题：函数的性质及应用,平面向量及应用
分析：首先将向量
MN
用
AB
，
AC
表示，然后求向量
MN
的平方，整理为关于n的二次函数的形式求最小值．
解答： 解：∵
MN
=
AN
-
AM
，
AM
=
1
2
(
AE
+
AF
)
AN
=
1
2
(
AB
+
AC
)，
∴
MN
=
1
2
(
AB
+
AC
-
AE
-
AF
)
=
1
2
[（1-m）
AB
+（1-n）
AC
]
∵m+n=1
∴
MN
=
1
2
[n
AB
+(1-n)
AC
]
|
MN
|2=
1
4
[n2
AB
2+2n（1-n）
AB
•
AC
+（1-n）2
AC
2]，
又
AB
•
AC
=|AB|×|AC|×cos120°=-
1
2
，
∴
MN
2=
1
4
[n2-n+n2+(1-n)2]=
1
4
（3n2-3n+1），n∈（0，1）
∴当n=
1
2
时，3n2-3n+1有最小值为
1
16

于是|
MN
|最小值为
1
4
．
故选C．
点评：本题给出含有120度等腰三角形中的向量，求向量
MN
模的最小值，着重考查了平面向量数量积公式及其运算性质和二次函数的最值求法等知识．
练习册系列答案
相关题目
已知圆O：x2+y2=25，点A（-3，0）、B（3，0），一条抛物线以圆O的切线为准线且过点A和B，则这列抛物线的焦点的轨迹方程是（　　）
A、
x2
25
+
y2
16
=1（x≠0）
B、
x2
25
+
y2
16
=1（y≠0）
C、
x2
25
+
y2
9
=1（x≠0）
D、
x2
25
+
y2
9
=1（y≠0）
已知函数f（x）=ax3+bx2+x+1在x=1处时取得极值为0，则ab=
 
．
圆ρ=
2
（cosθ+sinθ）的圆心坐标是（　　）
A、（
1
2
，
π
4
）
B、（1，
π
4
）
C、（
2
，
π
4
）
D、（2，
π
4
）
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0），过焦点垂直于长轴的弦长为1，且焦点与短轴两端点构成等边三角形．
（I）求椭圆的方程；
（Ⅱ）过点Q（-1，0）的直线l交椭圆于A，B两点，交直线x=-4于点E，
AQ
=λ
QB
，
AE
=μ
EB
．判断λ+μ是否为定值，若是，计算出该定值；不是，说明理由．
对于实数a，b，c，下列结论中正确的是（　　）
A、若a＞b，则ac2＞bc2
B、若a＞b＞0，则
1
a
＞
1
b
C、若a＜b＜0，则
b
a
＞
a
b
D、若a＞b，
1
a
＞
1
b
，则a＞0，b＜0
函数f（x）=sin2x+2
3
cos2x-
3
，函数g（x）=mcos（2x-
π
6
）-
3
2
m+2（m＞0），若对任意x1∈[0，
π
4
]，总存在x2∈[0，
π
4
]，使得g（x1）=f（x2）成立，则实数m的取值范围是
 
．
已知f（x）=x+lg
x
2-x
．
（1）求定义域；
（2）求f（x）+f（2-x）的值；
（3）猜想f（x）的图象具有怎样的对称性，并证明．
已知函数f（x）的导函数f′（x）=ax2+bx+c的图象如图，则f（x）的图象可能是（　　）
A、
B、
C、
D、

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网