题目内容
已知f(x)=x+lg
.
(1)求定义域;
(2)求f(x)+f(2-x)的值;
(3)猜想f(x)的图象具有怎样的对称性,并证明.
| x |
| 2-x |
(1)求定义域;
(2)求f(x)+f(2-x)的值;
(3)猜想f(x)的图象具有怎样的对称性,并证明.
考点:对数函数的图像与性质
专题:函数的性质及应用
分析:(1)根据对数函数的定义可以求出其定义域,
(2)利用对数的性质,计算即可.
(3)因为当x=1时,y=1,故猜想对称点为(1,1),然后再根据对称的性质证明即可.
(2)利用对数的性质,计算即可.
(3)因为当x=1时,y=1,故猜想对称点为(1,1),然后再根据对称的性质证明即可.
解答:
解:(1)由题意得,x(2-x)>0,
解得0<x<2,
∴函数f(x)的定义域为(0,2).
(2)∵f(x)=x+lg
,
∴f(x)+f(2-x)=x+lg
+2-x+lg
=2+lg
•
=2.
(3)关于点P(1,1)对称
证明:设Q(x,y)为函数图象上的任一点,
若Q点关于点P的对称点为Q1(x1,y1),
则
,即
,
∴f(x1)=x1+lg
=2-x+lg
=2-x-lg
=2-y=y1,
函数y=f(x)的图象关于点P(1,1)对称
解得0<x<2,
∴函数f(x)的定义域为(0,2).
(2)∵f(x)=x+lg
| x |
| 2-x |
∴f(x)+f(2-x)=x+lg
| x |
| 2-x |
| 2-x |
| x |
| x |
| 2-x |
| 2-x |
| x |
(3)关于点P(1,1)对称
证明:设Q(x,y)为函数图象上的任一点,
若Q点关于点P的对称点为Q1(x1,y1),
则
|
|
∴f(x1)=x1+lg
| x1 |
| 2-x1 |
| 2-x |
| x |
| x |
| 2-x |
函数y=f(x)的图象关于点P(1,1)对称
点评:本题主要考查对数函数的定义和对数的运算,以及图象的对称问题,属于中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
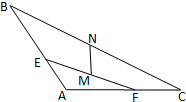 如图,△ABC中,AB=AC=1,∠A=120°,E,F分别是边AB,AC上的点,且
如图,△ABC中,AB=AC=1,∠A=120°,E,F分别是边AB,AC上的点,且| AE |
| AB |
| AF |
| AC |
| MN |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若xy<0,x,y∈R,则下列不等式中正确的是( )
| A、|x+y|>|x-y| |
| B、|x-y|<|x|+|y| |
| C、|x+y|<|x-y| |
| D、|x-y|<||x|-|y|| |
在(
-x2)6的展开式中,常数是( )
| 1 |
| x |
| A、20 | B、15 | C、-20 | D、-1 |