题目内容
已知圆O:x2+y2=25,点A(-3,0)、B(3,0),一条抛物线以圆O的切线为准线且过点A和B,则这列抛物线的焦点的轨迹方程是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:轨迹方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:设出切点与切线方程,可得a2+b2=25,设出焦点坐标,根据抛物线的定义求得点A,B到准线的距离等于其到焦点的距离,然后两式平方后分别相加和相减,联立后求得x和y的关系式.
解答:
解:设切点为(a,b),∴a2+b2=25,则切线为:ax+by-25=0
设焦点(x,y),由抛物线定义可得:
=
…①,
=
…②,
所以可得:
+
=1.
依题意焦点不能与A,B共线,∴y≠0.
所以这列抛物线的焦点的轨迹方程是
+
=1(y≠0).
故选B.
设焦点(x,y),由抛物线定义可得:
| (x-3)2+y2 |
| |3a-25| |
| 5 |
| (x+4)2+y2 |
| |3a+25| |
| 5 |
所以可得:
| x2 |
| 25 |
| y2 |
| 16 |
依题意焦点不能与A,B共线,∴y≠0.
所以这列抛物线的焦点的轨迹方程是
| x2 |
| 25 |
| y2 |
| 16 |
故选B.
点评:本题主要考查了抛物线的定义与椭圆的标准方程,考查了学生数形结合的思想及计算能力.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
函数f(x)=1-xlnx的零点所在区间是( )
A、(0,
| ||
B、(
| ||
| C、(1,2) | ||
| D、(2,3) |
已知f1(x)=sinx+cosx,fn+1(x)是fn (x)的导函数,即f2(x)=f′1(x),f3(x)=f′2(x),…,fn+1(x)=f′n(x),n∈N*,则f2012(x)=( )
| A、sinx+cosx |
| B、sinx-cosx |
| C、-sinx+cosx |
| D、-sinx-cosx |
设集合A=[x||x-1|<2},B={y|y2=2x,x∈[0,2]},则A∩B=( )
| A、[0,2] |
| B、(1,3) |
| C、(-1,2] |
| D、(1,4) |
已知{an}是公差不为0的等差数列,且an≥0;又定义bn=
+
(1≤n≤2003 ),则{bn}的最大项是( )
| an |
| a2004-n |
| A、b1001 |
| B、b1002 |
| C、b2003 |
| D、不能确定的 |
在等差数列{an}中,a1=15,d=-2,则a9=( )
| A、-1 | B、1 | C、2 | D、-3 |
在锐角△ABC中,BC=1,B=2A,则AC的取值范围为( )
A、(1,
| ||||
B、(
| ||||
C、(
| ||||
D、(2,
|
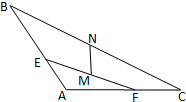 如图,△ABC中,AB=AC=1,∠A=120°,E,F分别是边AB,AC上的点,且
如图,△ABC中,AB=AC=1,∠A=120°,E,F分别是边AB,AC上的点,且