题目内容
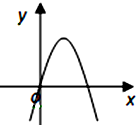
已知函数f（x）的导函数f′（x）=ax2+bx+c的图象如图，则f（x）的图象可能是（ ）
A、 |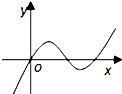
B、 |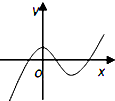
C、 |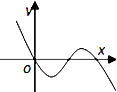
D、 |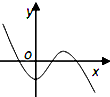
考点：函数的图象
专题：函数的性质及应用
分析：根据导数与原函数单调性间的关系判断：导数大于零则该函数为增函数，导数小于零则该函数为减函数．
解答：
解：根据导数与原函数单调性间的关系：从左到右分成三部分，
第一部分导数小于零，第二部分导数大于零，第三部分导数小于零，
则相应的，第一部分原函数为减函数，第二部分原函数为增函数，第三部分原函数为减函数；
满足题意只有C，D．
又因为f′（x）=3x2-2bx+2c经过原点，即c=0，
故选D．
第一部分导数小于零，第二部分导数大于零，第三部分导数小于零，
则相应的，第一部分原函数为减函数，第二部分原函数为增函数，第三部分原函数为减函数；
满足题意只有C，D．
又因为f′（x）=3x2-2bx+2c经过原点，即c=0，
故选D．
点评：本题主要考查导数法是如何利用函数的导数来刻画函数的单调性的，即：原函数的导数若大于零，则该函数在区间上是增函数；原函数的导数若小于零，则该函数在区间上是减函数．
练习册系列答案
相关题目
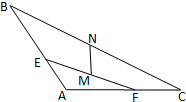如图，△ABC中，AB=AC=1，∠A=120°，E，F分别是边AB，AC上的点，且| AE |
| AB |
| AF |
| AC |
| MN |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在（
-x2）6的展开式中，常数是（ ）
| 1 |
| x |
| A、20 | B、15 | C、-20 | D、-1 |
若复数z=
的共轭复数为（ ）
| 2+i |
| 1+i |
A、
| ||
B、
| ||
C、
| ||
D、
|