题目内容
圆ρ=
(cosθ+sinθ)的圆心坐标是( )
| 2 |
A、(
| ||||
B、(1,
| ||||
C、(
| ||||
D、(2,
|
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:化极坐标方程为直角坐标方程,求出圆心的直角坐标,再由直角坐标求出极径后得答案.
解答:
解:由ρ=
(cosθ+sinθ),得ρ2=
ρcosθ+
ρsinθ,
即x2-
x+y2-
y=0,
∴圆ρ=
(cosθ+sinθ)的圆心的直角坐标为(
,
),
∴ρ=(
)2+(
)2=1.
∴圆ρ=
(cosθ+sinθ)的圆心坐标是(1,
).
故选:B.
| 2 |
| 2 |
| 2 |
即x2-
| 2 |
| 2 |
∴圆ρ=
| 2 |
| ||
| 2 |
| ||
| 2 |
∴ρ=(
| ||
| 2 |
| ||
| 2 |
∴圆ρ=
| 3 |
| π |
| 4 |
故选:B.
点评:本题考查了简单曲线的极坐标方程,考查了极坐标与直角坐标的互化,是基础题.

练习册系列答案
相关题目
设集合A=[x||x-1|<2},B={y|y2=2x,x∈[0,2]},则A∩B=( )
| A、[0,2] |
| B、(1,3) |
| C、(-1,2] |
| D、(1,4) |
若|
|=6,|
|=4,
•
=-12
,则
与
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、120° | B、150° |
| C、135° | D、45° |
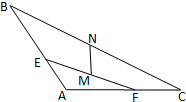 如图,△ABC中,AB=AC=1,∠A=120°,E,F分别是边AB,AC上的点,且
如图,△ABC中,AB=AC=1,∠A=120°,E,F分别是边AB,AC上的点,且| AE |
| AB |
| AF |
| AC |
| MN |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在(
-x2)6的展开式中,常数是( )
| 1 |
| x |
| A、20 | B、15 | C、-20 | D、-1 |