题目内容
函数f(x)=sin2x+2
cos2x-
,函数g(x)=mcos(2x-
)-
m+2(m>0),若对任意x1∈[0,
],总存在x2∈[0,
],使得g(x1)=f(x2)成立,则实数m的取值范围是 .
| 3 |
| 3 |
| π |
| 6 |
| 3 |
| 2 |
| π |
| 4 |
| π |
| 4 |
考点:三角函数中的恒等变换应用
专题:综合题,三角函数的图像与性质
分析:由x1∈[0,
],x2∈[0,
],可求得f(x)∈[1,2],g(x)∈[-m+2,-
m+2],进而由对任意x1∈[0,
],总存在x2∈[0,
],使得g(x1)=f(x2)成立,可得到关于m的不等式组,解之可求得实数m的取值范围.
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
解答:
解:∵f(x)=sin2x+2
cos2x-
=sin2x+
cos2x=2sin(2x+
),
当x∈[0,
],2x+
∈[
,
],
∴2sin(2x+
)∈[1,2],
∴f(x)∈[1,2],
对于g(x)=mcos(2x-
)-
m+2(m>0),2x-
∈[-
,
],
mcos(2x-
)∈[
,m],
∴g(x)∈[-m+2,-
m+2],
若对任意x1∈[0,
],总存在x2∈[0,
],使得g(x1)=f(x2)成立,
则-m+2≥1,-
m+2≤2,
解得实数m的取值范围是:[0,1],
故答案为:[0,1]
| 3 |
| 3 |
| 3 |
| π |
| 3 |
当x∈[0,
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
∴2sin(2x+
| π |
| 3 |
∴f(x)∈[1,2],
对于g(x)=mcos(2x-
| π |
| 6 |
| 3 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
mcos(2x-
| π |
| 6 |
| m |
| 2 |
∴g(x)∈[-m+2,-
| 1 |
| 2 |
若对任意x1∈[0,
| π |
| 4 |
| π |
| 4 |
则-m+2≥1,-
| 1 |
| 2 |
解得实数m的取值范围是:[0,1],
故答案为:[0,1]
点评:本题考查两角和与差的正弦函数,着重考查三角函数的性质的运用,考查二倍角的余弦,解决问题的关键是理解对任意x1∈[0,
],总存在x2∈[0,
],使得g(x1)=f(x2)成立的含义,属于难题.
| π |
| 4 |
| π |
| 4 |

练习册系列答案
相关题目
在锐角△ABC中,BC=1,B=2A,则AC的取值范围为( )
A、(1,
| ||||
B、(
| ||||
C、(
| ||||
D、(2,
|
若|
|=6,|
|=4,
•
=-12
,则
与
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、120° | B、150° |
| C、135° | D、45° |
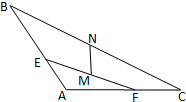 如图,△ABC中,AB=AC=1,∠A=120°,E,F分别是边AB,AC上的点,且
如图,△ABC中,AB=AC=1,∠A=120°,E,F分别是边AB,AC上的点,且| AE |
| AB |
| AF |
| AC |
| MN |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
一个正方体的顶点都在球面上,它的棱长为2cm,则球的表面积是( )
| A、8πcm2 |
| B、12πcm2 |
| C、16πcm2 |
| D、20πcm2 |