题目内容
已知抛物线y2=2px(p>0)的准线方程是x=-1
(1)求抛物线的标准方程和焦点坐标.
(2)求直线y=x和抛物线所围成的平面图形的面积.
(1)求抛物线的标准方程和焦点坐标.
(2)求直线y=x和抛物线所围成的平面图形的面积.
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)由抛物线的焦点坐标和准线方程,求出p即可.
(2)先联立求出方程组的解,利用导数的运算法则和微积分基本定理即可得出.
(2)先联立求出方程组的解,利用导数的运算法则和微积分基本定理即可得出.
解答:
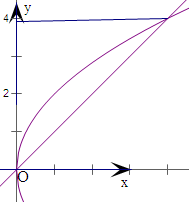 解:(1)由抛物线y2=2px(p>0)的准线方程是x=-1,
解:(1)由抛物线y2=2px(p>0)的准线方程是x=-1,
则p=2,故抛物线的标准方程是y2=4x,焦点坐标为(1,0).
(2)由
解得
,
则直线y=x和抛物线所围成的平面图形的面积S=
(y-
y2)dy
=(
y2-
y3)|
=
×16-
×64
=8-
=
.
 解:(1)由抛物线y2=2px(p>0)的准线方程是x=-1,
解:(1)由抛物线y2=2px(p>0)的准线方程是x=-1,则p=2,故抛物线的标准方程是y2=4x,焦点坐标为(1,0).
(2)由
|
|
|
则直线y=x和抛物线所围成的平面图形的面积S=
| ∫ | 4 0 |
| 1 |
| 4 |
=(
| 1 |
| 2 |
| 1 |
| 12 |
4 0 |
| 1 |
| 2 |
| 1 |
| 12 |
=8-
| 16 |
| 3 |
| 8 |
| 3 |
点评:本题考查抛物线的标准方程和焦点及准线,考查定积分求面积,熟练掌握导数的运算法则和微积分基本定理是解题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
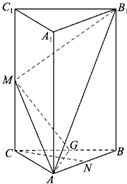 如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点.且CC1=
如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点.且CC1=