题目内容
在某次考试中,甲,乙,丙三人合格(互不影响)的概率分别是
,
,
.考试结束后,最容易出现几人合格的情况?
| 2 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
考点:互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:设X表示合格人数,则X=0,1,2,3,分别求出相应的概率,由此能求出结果.
解答:
解:设A表示“甲合格”,B表示“乙合格”,C表示“丙合格”,
则P(A)=
,P(B)=
,P(C)=
,
设X表示合格人数,则X=0,1,2,3,
P(X=0)=(1-
)(1-
)(1-
)=
,
P(X=1)=
(1-
)(1-
)+(1-
)×
×(1-
)+(1-
)×(1-
)×
=
,
P(X=2)=(1-
)×
×
+
(1-
)×
+
×
×(1-
)=
,
P(X=3)=
×
×
=
.
∴最容易出现1人合格的情况.
则P(A)=
| 2 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
设X表示合格人数,则X=0,1,2,3,
P(X=0)=(1-
| 2 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 10 |
P(X=1)=
| 2 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
| 25 |
| 60 |
P(X=2)=(1-
| 2 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
| 23 |
| 60 |
P(X=3)=
| 2 |
| 5 |
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 10 |
∴最容易出现1人合格的情况.
点评:本题考查概率的求法,是基础题,解题时要认真审题.

练习册系列答案
相关题目
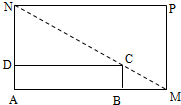 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米.
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米.