题目内容

设tan（α+
8π
7
）=a，求
sin(
15
7
π+α)+3cos(α-
13
7
π)
sin(
20π
7
-a)-cos(α+
22π
7
)
的值．
考点：运用诱导公式化简求值,同角三角函数基本关系的运用
专题：计算题,三角函数的求值
分析：由tan（α+
8π
7
）=a，可得tan（
π
7
+α）=a，从而有诱导公式可得
sin(
15
7
π+α)+3cos(α-
13
7
π)
sin(
20π
7
-a)-cos(α+
22π
7
)
=
a+3
a+1
．
解答： 解：∵tan（α+
8π
7
）=a，∴tan（
π
7
+α）=a．
∴
sin(
15
7
π+α)+3cos(α-
13
7
π)
sin(
20π
7
-a)-cos(α+
22π
7
)
=
sin(
π
7
+α)+3cos(
π
7
+α)
sin(
π
7
+α)+cos(
π
7
+α)
=
tan(
π
7
+α)+3
tan(
π
7
+α)+1
=
a+3
a+1
．
点评：本题主要考查了运用诱导公式化简求值，同角三角函数基本关系的运用，属于基本知识的考查．
练习册系列答案
相关题目
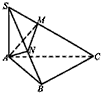如图，在△ABC中，∠B=90°，SA⊥平面ABC，点A在SB和SC上的射影分别为N，M．求证：MN⊥SC．
已知空间四点A、B、C、D共面，若对空间中任一点O有x
OA
+y
OB
+z
OC
+
OD
=
0
，则x+y+z=
 
．
直线l：y=
3
x经过曲线C：y=
3
sinωx（ω＞0）在区间[0，+∞）上的第一个最高点，则曲线C的最小正周期是（　　）
A、4πB、2πC、4D、2
化简：sin（x+
π
3
）+2sin（x-
π
3
）-
3
cos（
2π
3
-x）．
求函数y=
2x+1-1
2x+1
的值域．
已知过点A（1，0）的动直线依次交抛物线x2=2y、直线y=x于点B、C、D，求证：
AB
AD
=
CB
CD
．
在锐角△ABC中，a，b，c分别为角A、B、C所对的边，且
3
a=2csinA．
（Ⅰ）确定角C的大小；
（Ⅱ）若c=
7
，且△ABC的面积为
3
3
2
，求a+b的值．
当实数x，y满足约束条件
x≥1
y≥1
x+y≤7
时，z=x-y的最大值为m，则对于正数a，b，若
1
a
+
1
b
=m，则a+b的最小值是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网