题目内容
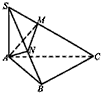 如图,在△ABC中,∠B=90°,SA⊥平面ABC,点A在SB和SC上的射影分别为N,M.求证:MN⊥SC.
如图,在△ABC中,∠B=90°,SA⊥平面ABC,点A在SB和SC上的射影分别为N,M.求证:MN⊥SC.考点:直线与平面垂直的性质
专题:空间位置关系与距离
分析:首先,证明BC⊥平面SAB,然后,从而得到AN⊥BC;对于MN⊥SC的证明,可以先证明SC⊥平面AMN,然后,很容易得到MN⊥SC.
解答:
证明:∵SA⊥面ABC,BC⊆平面ABC,
∴SA⊥BC,
又∵AB⊥BC,SA∩AB=A,
∴BC⊥平面SAB,
∵AN⊆平面SAB,
∴AN⊥BC;
∵AN⊥SB,且SB∩BC=B,
∴AN⊥平面SBC,
∵SC⊆平面SBC,
∴SC⊥AN,又AM⊥SC,且AM∩AN=A,
∴SC⊥平面AMN,
∴MN⊥SC.
∴SA⊥BC,
又∵AB⊥BC,SA∩AB=A,
∴BC⊥平面SAB,
∵AN⊆平面SAB,
∴AN⊥BC;
∵AN⊥SB,且SB∩BC=B,
∴AN⊥平面SBC,
∵SC⊆平面SBC,
∴SC⊥AN,又AM⊥SC,且AM∩AN=A,
∴SC⊥平面AMN,
∴MN⊥SC.
点评:本题重点考查了空间中直线与平面垂直,直线与直线垂直等位置关系,解题关键是线面垂直和线线垂直的相互转化,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列命题错误的是( )
| A、命题“若x2=1,则x=1”的否命题为“若x2≠1,则x≠1” |
| B、若命题p:?x0∈R,x02-x0+1≤0,则¬p:?x∈R,x2-x+1>0 |
| C、△ABC中,sinA>sinB是A>B的充要条件 |
| D、若p∨q为真命题,则p、q均为真命题 |
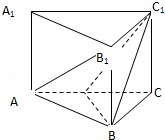 已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点.
已知正三棱柱ABC-A1B1C1的底面边长为8,侧棱长为6,D为AC中点. 如图,P为平行四边形ABCD所在平面外一点,平面PAD∩平面PBC=m.求证:BC∥m.
如图,P为平行四边形ABCD所在平面外一点,平面PAD∩平面PBC=m.求证:BC∥m.