题目内容
已知过点A（1，0）的动直线依次交抛物线x2=2y、直线y=x于点B、C、D，求证：
=
．
| AB |
| AD |
| CB |
| CD |
考点：直线与圆锥曲线的关系
专题：圆锥曲线的定义、性质与方程
分析：分别过B，C，D作x轴的垂线，垂足分别为B1（x1，0），C1（x2，0），D1（x3，0），则
=
等价于
=
，设过点A的动直线方程为y=k（x-1），联立抛物线方程及y=x，可用k表示交点的横坐标x1，x2，x3，化简即可得证．
| AB |
| AD |
| CB |
| CD |
| 1-x1 |
| 1-x3 |
| x1-x2 |
| x2-x3 |
解答：
证明：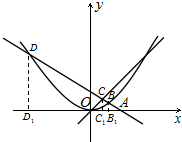
分别过B，C，D作x轴的垂线，垂足分别为B1（x1，0），C1（x2，0），D1（x3，0），
如右图所示．
依题意，设过点A的动直线方程为y=k（x-1），显然k≠0，
由
，消去y，得x2-2kx+2k=0，
解得x1=k+
，x3=k-
．
由于直线y=k（x-1）与直线y=x相交，故k≠1，联立此两方程得x2=
．
易知BB1∥CC1∥DD1，所以
=
，
=
=
=
=
．
故
=
，得证．
分别过B，C，D作x轴的垂线，垂足分别为B1（x1，0），C1（x2，0），D1（x3，0），如右图所示．
依题意，设过点A的动直线方程为y=k（x-1），显然k≠0，
由
|
解得x1=k+
| k2-2k |
| k2-2k |
由于直线y=k（x-1）与直线y=x相交，故k≠1，联立此两方程得x2=
| k |
| 1-k |
易知BB1∥CC1∥DD1，所以
| AB |
| AD |
1-k-
| ||
1-k+
|
| CB |
| CD |
k+
| ||||
|
k2-2k+(k-1)
| ||
(k-1)
|
=
| ||||
|
1-k-
| ||
1-k+
|
故
| AB |
| AD |
| CB |
| CD |
点评：本题考查了直线与抛物线的交点问题及比例的性质，关键是将线段之比转化为交点横坐标的差之比．
练习册系列答案
名校课堂系列答案
相关题目