题目内容
12.已知椭圆C:$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,点$P(\sqrt{2},2)$在椭圆上.(1)求椭圆C的方程;
(2)过椭圆上的焦点F作两条相互垂直的弦AC,BD,求|AC|+|BD|的取值范围.
分析 (1)由椭圆的离心率为$\frac{{\sqrt{2}}}{2}$,点$P(\sqrt{2},2)$在椭圆上,列出方程组得a2=8,b2=4.由此能求出椭圆方程.
(2)当直线AC,BD中一条直线斜率不存在时,|AC|+|BD|=$6\sqrt{2}$.当直线AC,BD斜率均存在时,设直线AC的方程为:y=kx+2,联立$\left\{\begin{array}{l}\frac{y^2}{8}+\frac{x^2}{4}=1\\ y=kx+2\end{array}\right.$,得(k2+2)x2+4kx-4=0,由韦达定理得|AC|=$\frac{{4\sqrt{2}({{k^2}+1})}}{{{k^2}+2}}$,用$-\frac{1}{k}$代换上式中的k可得$|{BD}|=\frac{{4\sqrt{2}({{k^2}+1})}}{{2{k^2}+1}}$,由此能求出|AC|+|BD|的取值范围.
解答 解:(1)因为$e=\frac{c}{a}=\frac{{\sqrt{{a^2}-{b^2}}}}{a}=\frac{{\sqrt{2}}}{2}$,所以a2=2b2.
又$P(\sqrt{2},2)$在椭圆上,所以$\frac{4}{a^2}+\frac{2}{b^2}=1$.
联立上述方程,解得a2=8,b2=4.
所以椭圆方程为$\frac{y^2}{8}+\frac{x^2}{4}=1$.
(2)当直线AC,BD中一条直线斜率不存在时,|AC|+|BD|=$6\sqrt{2}$.
当直线AC,BD斜率均存在时,
不妨设直线AC的斜率为k,显然k≠0,则lAC:y=kx+2,
联立$\left\{\begin{array}{l}\frac{y^2}{8}+\frac{x^2}{4}=1\\ y=kx+2\end{array}\right.$,得(k2+2)x2+4kx-4=0
设A(x1,y1),C(x2,y2),则${x_1}+{x_2}=\frac{-4k}{{{k^2}+2}}$,${x_1}{x_2}=\frac{-4}{{{k^2}+2}}$,
$|{AC}|=\sqrt{1+{k^2}}|{{x_1}-{x_2}}|$=$\frac{{4\sqrt{2}({{k^2}+1})}}{{{k^2}+2}}$,
由于直线BD的斜率为$-\frac{1}{k}$,用$-\frac{1}{k}$代换上式中的k可得$|{BD}|=\frac{{4\sqrt{2}({{k^2}+1})}}{{2{k^2}+1}}$
于是|AC|+|BD|=$\frac{{4\sqrt{2}({{k^2}+1})}}{{{k^2}+2}}+$$\frac{{4\sqrt{2}({{k^2}+1})}}{{2{k^2}+1}}$=$\frac{{12\sqrt{2}{{({{k^2}+1})}^2}}}{{({{k^2}+2})({2{k^2}+1})}}$.
令t=k2+1>1,则|AC|+|BD|=$\frac{{12\sqrt{2}{t^2}}}{{(2t-1)({t+1})}}=\frac{{12\sqrt{2}}}{{2+\frac{1}{t}-\frac{1}{t^2}}}$,
因为$2+\frac{1}{t}-\frac{1}{t^2}$=$-{(\frac{1}{t}-\frac{1}{2})^2}+\frac{9}{4}$$∈({2,\frac{9}{4}}]$,
所以|AC|+|BD|=$\frac{{12\sqrt{2}}}{{2+\frac{1}{t}-\frac{1}{t^2}}}$$∈[\frac{{16\sqrt{2}}}{3},6\sqrt{2})$.
综上所述,|AC|+|BD|的取值范围为$[{\frac{{16\sqrt{2}}}{3},6\sqrt{2}}]$.
点评 本题考查椭圆方程、两线段和的取值范围、椭圆性质、直线方程等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是中档题.

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案| A. | -3<k<1 | B. | k>1 | C. | -1<k<1 | D. | -1<k<3 |
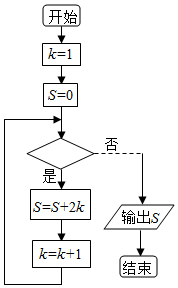 如果执行如图的程序框图,输出的S=30,则判断框处为( )
如果执行如图的程序框图,输出的S=30,则判断框处为( )| A. | k<5 | B. | k≤5 | C. | k≥6 | D. | k>6 |
 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.图1是源于其思想的一个程序框图,若输入的a,b分别为4,2,则输出的n等于( )
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.图1是源于其思想的一个程序框图,若输入的a,b分别为4,2,则输出的n等于( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
| A. | -4 | B. | -1 | C. | 2 | D. | 5 |
| A. | (0,1] | B. | (0,1) | C. | (1,+∞) | D. | [1,+∞) |
| A. | (0,+∞) | B. | (1,2) | C. | (2,+∞) | D. | (-∞,0) |
| A. | x1+x2=8 | B. | x1+x2=4 | C. | y1+y2=8 | D. | y1+y2=4 |