题目内容

16．已知抛物线C：y2=8x的焦点为F，过F的直线l与抛物线C交于M（x1，y1），N（x2，y2）两点，若|MN|=8，则（　　）
A．x1+x2=8B．x1+x2=4C．y1+y2=8D．y1+y2=4

分析 根据抛物线方程可求得准线方程，进而根据抛物线的定义可知|MN|=x1+x2+p，求解即可．

解答 解：依题意可知p=4，
准线方程为x=-2，
根据抛物线的定义，
可知|MN|=x1+2+x2+2=8．
可得x1+x2=4．
故选：B．

点评 本题主要考查抛物线的应用．属基础题．

练习册系列答案
相关题目
12．已知椭圆C：$\frac{y^2}{a^2}+\frac{x^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{2}}}{2}$，点$P（\sqrt{2}，2）$在椭圆上．
（1）求椭圆C的方程；
（2）过椭圆上的焦点F作两条相互垂直的弦AC，BD，求|AC|+|BD|的取值范围．
13．已知向量$\overrightarrow{a}$=（-4，x），$\overrightarrow{b}$=（1，2），若$\overrightarrow{a}$⊥$\overrightarrow{b}$，则x=2．
4．设数列{an}满足a1=$\frac{1}{3}$，an+1=an+$\frac{{a}_{n}^{2}}{{n}^{2}}$，n∈N，*
（1）求a2，a3；
（2）证明：数列{an}为递增数列
（3）证明：$\frac{n}{2n+1}$≤an$≤\frac{2n-1}{2n+1}$，n∈N*．
11．设向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=3，|$\overrightarrow{a}$-$\overrightarrow{b}$|=1，$\overrightarrow{a}$与$\overrightarrow{b}$夹角为θ，则$\frac{|\overrightarrow{a}|}{|\overrightarrow{b}|cosθ}$+$\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|cosθ}$=（　　）
A．$\frac{1}{2}$B．$\frac{5}{2}$C．$\frac{5}{4}$D．3
1．已知点P为一动点，点A的坐标为（1，$\frac{3}{2}$），点B的坐标为（1，-$\frac{3}{2}$）．两条不同的直线PA、PB与x轴交点的横坐标分别为m、n且满足mn=4，记动点P的轨迹及A，B两点组成曲线C，设过点（0，1）且斜率为k的直线l与曲线C交于不同的两点M，N，线段MN的中点为E点，直线OE与曲线C交于Q、R两点．
（1）求曲线C的方程；
（2）若|EM|•|EN|=λ|EQ|•|ER|，求实数λ的取值范围．
8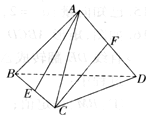．如图，正四面体ABCD中，E、F分别是棱BC和AD的中点，则直线AE和CF所成的角的余弦值为（　　）
A．$\frac{1}{3}$B．$\frac{2}{3}$C．$\frac{1}{4}$D．$\frac{3}{4}$
5．设函数f（x）=|x2-2x-1|，若m＞n＞1，且f（m）=f（n），则mn的取值范围为（　　）
A．$（{3，3+2\sqrt{2}}）$B．$（{3，3+2\sqrt{2}}]$C．（1，3）D．（1，3]
6．计算$\frac{{{{sin}^2}15°}}{tan15°}$=$\frac{1}{4}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网